|
★ ☆ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
I numeri razionali
Le frazioni
Regole delle frazioni
I numeri razionali
Simbolo: ℚ
Cardinalità: ℵ0. L'insieme dei numeri razionali e l'insieme dei numeri naturali possono esser messi in corrispondenza biunivoca.
Definizione: l'insieme dei numeri razionali si definisce allargando l'insieme dei numeri interi, con l'introduzione dei reciproci dei numeri interi, nel seguente modo:
|
Il reciproco di un numero intero "a" ≠ 0 è quel numero "b" ≠ 0 tale che:
a × b = 1
|
Il reciproco di a si indica con a ⁻¹, e possiede molte proprietà, ad esempio:
L'insieme dei numeri razionali quindi contiene:
- i numeri interi (positivi, zero e negativi)
- i reciproci dei numeri interi, tranne dello zero (anch'essi positivi e negativi);
- tutti i prodotti tra numeri interi e loro reciproci.
Operazioni: l'addizione, la sottrazione, la moltiplicazione e la potenza tra numeri razionali sono ben definite, si possono sempre fare all'interno di ℚ e il risultato che si ottiene è sempre un numero razionale; per svolgerele operazioni tra numeri razionali possiamo aiutarci con le regole delle frazioni (vedi sotto).
Al contrario le altre operazioni non sono ben definite, si possono fare solo sotto alcune limitazioni:
- la divisione si può fare solo se il divisore è diverso da zero; come abbiamo visto, dividere un numero a per b, equivale a moltiplicare a per il reciproco di b;
- la radice con indice pari si può fare solo se il radicando è positivo ed è una potenza di esponente multiplo dell'indice della radice;
- la radice con indice dispari si può fare solo se il radicando è una potenza di esponente multiplo dell'indice della radice;
- il logaritmo si può fare solo se l'argomento è positivo ed è una potenza della base.
Di fatto valgono le stesse limitazioni dei numeri interi, con la sola eccezione della divisione, che si può fare quasi sempre.
Proprietà: dalla definizione si osserva che l'insieme ℚ è congruente a ℤ × ℤ, e quindi a ℕ × ℕ (dove in questo caso × indica il prodotto cartesiano tra due insiemi); quindi anche l'insieme ℚ è ordinato, infinito e numerabile: ℚ può esser messo in corrispondenza biunivoca con ℕ (tuttavia non è facile descrivere una possibile corrispondenza).
A differenza di ℕ e ℤ, ℚ non è discreto: è un insieme denso, in quanto ogni coppia di numeri razionali ha sempre un altro numero razionale tra loro.
Osserviamo inoltre che l'insieme dei numeri razionali positivi non possiede un elemento minimo, un numero più piccolo rispetto a tutti gli altri: un numero razionale può esser piccolo a piacere! Analogamente i numeri razionali negativi non hanno un numero massimo.
Dal punto di vista algebrico, ℚ è un campo rispetto alla somma e al prodotto: infatti
(ℚ, +) e (ℚ*, ×) sono gruppi commutativi, essendo ℚ* l'insieme di tutti i razionali escluso lo zero.
^
Torna su
Le frazioni
Come abbiamo visto, l'insieme dei numeri razionali contiene tutti i possibili prodotti tra i numeri interi e i reciproci; equivalentemente ogni numero razionale corrisponde al quoziente tra due numeri interi, purché il secondo diverso da zero; a sua volta ogni divisione può esser scritta in forma di frazione:
Da questo segue che:
|
Ogni numero razionale si può scrivere sotto forma di frazione.
|
Il risultato numerico di una frazione è quindi il quoziente di una divisione, un rapporto a ∶ b, e può esser un numero intero, oppure un numero decimale periodico (limitato o illimitato).
La parola razionale deriva infatti dal latino ratio, che vuol dire rapporto (oltre ad avere altri significati, come calcolo, ragionamento, causa). L'insieme dei numeri razionali è quindi l'insieme di tutti i rapporti tra numeri interi, tutti i quozienti della divisione tra numeri interi.
In una frazione il primo termine, quello sopra si chiama numeratore , mentre il secondo, quello sotto si chiama denominatore .
Trasformazione di un numero razionale, da decimale a frazione
Ogni numero razionale può esser scritto come numero decimale limitato, oppure come illimitato periodico; in entrambi i casi è utile saper ricavare una frazione equivalente al numero decimale.
|
Esempio 4 a. Trasformiamo il numero 15,837
Esso possiede cinque cifre, di cui tre sono decimali; al numeratore mettiamo 15837 (senza la virgola) e al denominatore 1000 (tre 0 in quanto sono tre le cifre decimali).
|
|
Esempio 4 b. Trasformiamo il numero 175,31
Esso possiede tre cifre intere e due cifre decimali del periodo; al numeratore mettiamo la differenza tra 17531 (senza la virgola) meno 175 (le cifre intere), mentre al denominatore 99 (due 0 in quanto sono due le cifre del periodo).
| 175,31 = |
17531 − 17599 |
= |
1735699 |
|
|
Esempio 4 c. Trasformiamo il numero 5,14912
Esso possiede una cifra intera tre cifre nell'antiperiodo e due cifre nel periodo; al numeratore mettiamo la differenza tra 514912 (senza la virgola) meno 5149 (le cifre non periodiche), mentre al denominatore 99000 (due 9 per le le cifre del periodo e tre 0 per le cifre dell'antiperiodo).
| 5,14912 = |
514912 − 514999000 |
= |
50976399000 |
|
Ma cosa rappresenta una frazione?
Una frazione rappresenta una parte, una porzione, una percentuale rispetto ad un qualcosa; questo "qualcosa" in genere, se non diversamente specificato, è l'unità, il numero 1.
Per familiarizzare meglio con le frazioni, è utile vedere il denominatore della frazione come un valore di riferimento: è lui a dirci quale porzione dell'unità dobbiamo usare come riferimento; le frazioni più semplici sono le frazioni unitarie, ossia quelle che hanno 1 al numeratore, ad esempio:
1 / 2 è una parte corrispondente alla metà di uno; quindi occorrono 2 parti per formare uno.
1 / 3 corrisponde all terza parte uno; quindi ne occorrono tre per formare uno.
1/ 10 corrisponde alla decima parte di uno; quindi ne occorrono 10 per ottenere l'intero.
Le frazioni unitarie possono esser viste come sottomultipli dell'unità.
|
Esempio 5. Vediamo due esempi pratici.
Ragioniamo con gli euro
Cosa sono i centesimi di euro?
Un centesimo è (come dice la parola) la centesima parte di un euro, quindi se ho cento centesimi ottengo un intero, quindi un euro; se ho 150 centesimi ho più di un euro, perché ho più parti di quelle necessarie.
Al contrario se ho 80 centesimi ho meno di un euro; di fatto dire ottanta centesimi corrisponde a dire prendo un euro, lo divido in 100 parti e ne prendo 80, proprio come si fa con le frazioni.
Ragioniamo con i minuti e le ore
Cos'è un quarto d'ora?
È la quarta parte di un'ora, occorrono 4 quarti d'ora per formare un'ora completa; se ho un solo quarto d'ora, so che corrisponde a 15 minuti, poiché un'ora corrisponde a 60 minuti, e 60 ∶ 4 = 15.
Similmente dire 2 quarti d'ora vuol dire la metà di un'ora, ossia 30 minuti, e 3 quarti d'ora vuol dire 45 minuti, in quanto devo prendere 3 parti da 15 minuti.
|
Vediamo graficamente alcuni semplici esempi di frazioni:
| Esempio |
|
Esempio |
|
Figura 1 |
|
Figura 2 |
|
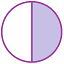Figura 3 |
|
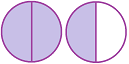Figura 4 |
|
Figura 5 |
|
Figura 6 |
|
Figura 7 |
|
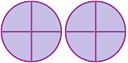Figura 8 |
|
Se quindi scriviamo 2 / 5, indichiamo che stiamo lavorando con quantità di valore corrispondente alla quinta parte di un intero, e che di esse ne stiamo contando 2.
Torniamo ora alle relazioni con i numeri razionali.
in particolare:
- lo zero si può scrivere come una frazione avente al numeratore zero e al denominatore un qualunque altro numero (tranne lo zero stesso);
- ogni numero intero si può scrivere come una frazione avente al numeratore tale numero e al denominatore uno;
- l'opposto di una frazione corrisponde ad una frazione avente stesso denominatore e numeratore opposto rispetto a quello iniziale;
- il reciproco di una frazione si scrive come una frazione con numeratore e denominatore scambiati tra loro di posto.
Attenzione: il denominatore non può essere zero, infatti non si può dividere per zero, in quanto, come abbiamo visto, zero non è il reciproco di alcun numero e non possiede reciproco. Scrivere zero al denominatore è un errore, poiché una tale frazione non ha significato matematico.
^
Torna su
Regole delle frazioni
Due frazioni sono equivalenti se sono rapporti in proporzione, ossia se permettono di ottenere lo stesso quoziente. Come si ottengono frazioni equivalenti?
Proprietà invariantiva
Se moltiplichiamo o dividiamo numeratore e denominatore di una frazione per uno stesso numero (diverso da zero) otteniamo una frazione equivalente a quella iniziale. |
Quindi ad esempio:
Infatti da un punto di vista logico, prendere 2 pezzi di valore un quinto corrisponde a prenderne 6 di valore un quindicesimo o anche 20 di valore un cinquantesimo ciascuno.
Una frazione si dice ridotta o semplificata se il numeratore e il denominatore sono stati divisi entrambi per un fattore comune (maggiore di 1); in particolare è ridotta ai minimi termini se il numeratore e il denominatore ottenuti non hanno più fattori in comune (maggiori di 1) per cui esser divisi entrambi.
Osservazione: per poter ridurre una frazione ai minimi termini, è necessario scomporre in fattori il numeratore e il denominatore, in modo da poter semplificare la frazione, dividendo entrambi per i fattori in comune (a meno che l'unico fattore in comune sia 1); non è necessario in effetti effettuare una scomposizione completa di numeratore e denominatore in fattori primi (anche se questa è molto utile), è sufficiente indivuduare un fattore comune.
La frazione così semplificata in alcuni casi può tuttavia può non esser ridotta ai minimi termini e, qualora si trovassero ulteriori fattori in comune, può esser nuovamente ridotta; per ottenere subito una frazione ridotta ai minimi termini occore individuare il M.C.D. tra numeratore e denominatore e dividere entrambi per esso.
|
Esempio 6. Vogliamo semplificare la frazione seguente:
Procediamo in modo lento, semplificando un fattore alla volta: per prima cosa ci accorgiamo che numeratore e denominatore sono entrambi divisibili per 2:
Anche questa frazione, sebbene ridotta, può esser ulteriormente semplificata dividendo sopra e sotto ancora per 2:
Anche questa terza frazione può esser ulteriormente semplificata dividendo sopra e sotto ancora per 3:
Questa frazione è formata da numeri che non si possono più dividere, quindi è ridotta ai minimi termini.
Osserviamo che lo stesso risultato si può ottenere calcolando il M.C.D. tra numeratore e denomintare iniziali:
M.C.D.(24, 36) = 12
e semplificando la frazione dividendo direttamente per 12:
|
Operazioni: le operazioni tra frazioni seguono le limitazioni viste in generale per i numeri razionali.
- Addizione: se due frazioni hanno lo stesso denominatore, la loro somma è una frazione avente lo stesso denominatore, e come numeratore la somma tra i numeratori (come quando addizioniamo due valori con la stessa unià di misura).
Se non hanno lo stesso denominatore, possiamo trasformarle in altre frazioni (equivalenti) con lo stesso denominatore; tale denominatore può essere un qualunque multiplo comune di entrambi i denominatori, ma in generale è meglio usare il loro m.c.m.
- Sottrazione: come avviene con i numeri interi, per ottenere la differenza tra due frazioni è sufficiente addizionare alla prima l'opposto della seconda.
- Moltiplicazione: il prodotto tra due frazioni si ottiene moltiplicando direttamente i due numeratori tra loro e i due denominatori tra loro; ovviamente è utile, prima di effettuare una moltiplicazione, controllare se ogni numeratore abbia fattori in comune con qualche denominatore, per poter esser semplificati.
- Divisione: come abbiamo visto con i numeri razionali, per ottenere il quoziente tra due frazioni è sufficiente moltiplicare alla prima il reciproco della seconda.
- Elevamento a potenza la potenza di una frazione, è una frazione avente per numeratore e denominatore le potenze di quelli iniziali.
- Estrazione di radice la radice di una frazione, è una frazione avente per numeratore e denominatore le radici di quelli iniziali.
- Logaritmo il logaritmo di una frazione corrisponde alla differenza tra il logaritmo del numeratore e quello del denominatore.
Vediamo alcuni esempi in cui svolgiamo calcoli tra frazioni.
|
Esempio 7.
Il m.c.m. tra i denominatori è 36; occorre quindi modificare le due frazioni, trasformandole in due frazioni equivalenti a quellle iniziali, ma con denominatore 36.
Per aiutarci, osserviamo che 36 = 9 × 4, quindi nella prima frazione il numeratore e il denominatore devono esser moltiplicati per 4:
Analogamente nella altre frazioni il numeratore e il denominatore devono esser moltiplicati numeri opportuni:
| 16 |
≡ |
1 · 66 · 6 |
≡ |
636 |
| 512 |
≡ |
5 · 312 · 3 |
≡ |
1536 |
A questo punto possiamo addizionare le due frazioni, operando solamente tra i numeratori:
|
|
Esempio 8.
Il m.c.m. tra i denominatori è 6; osserviamo che il primo termine è un numero intero, quindi si può scrivere come una frazione avente denominatore 1.
trasformiamo tutti i termini, mettendo denominatore 6.
| 51 |
≡ |
5 · 61 · 6 |
≡ |
306 |
| 13 |
≡ |
1 · 23 · 2 |
≡ |
26 |
| 72 |
≡ |
7 · 32 · 3 |
≡ |
216 |
| 56 |
≡ |
5 · 16 · 1 |
≡ |
56 |
A questo punto possiamo addizionare le due frazioni, operando solamente tra i numeratori:
| 306 |
+ |
26 |
− |
216 |
+ |
56 |
= |
166 |
≡ |
83 |
|
|
Esempio 9. Svolgiamo la seguente espressione.
Seguendo il normale ordine delle operazioni, vanno svolte prima moltiplicazioni e divisioni; possiamo iniziare invertendo la divisione, trasformandola in moltiplicazione e facendo il reciproco dell'ultima frazione:
Prima di svolgere le moltiplicazioni, osserviamo che possiamo semplificare i numeratori e i denominatori "a croce":
| 59 |
× |
125 |
+ |
154 |
× |
169 |
= |
| = |
13 |
× |
41 |
+ |
51 |
× |
43 |
= |
| = |
43 |
+ |
203 |
A questo punto possiamo addizionare le due frazioni, osservando che il denominatore è uguale, per cui operiamo solamente tra i numeratori:
|
^
Torna su
<<< Precedente -
Successivo >>>
|
