★ ★ ☆

CONTENUTO DELLA PAGINA
La Trigonometria
La misura degli angoli
Sotto-sezioni

La Trigonometria

La parola 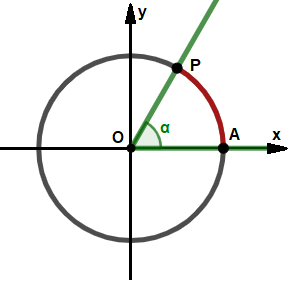Trigonometria deriva dal greco: Τριγωνον (trigonon = triangolo) + μετρον (metron = misura); questa sezione è dedicata quindi allo studio dei triangoli.
Una parte fondamentale è la Goniometria ossia lo studio degli angoli e le relative applicazioni.

Punto di partenza della trigonometria è la circonferenza goniometrica, una circonferenza del piano cartesiano, avente raggio unitario e centro nell'origine degli assi (vedi figura 1).
Tale circonferenza ha quindi equazione:

x² + y² = 1

Lo studio della trigonometria riguarda proprietà geometriche e analitiche legate all'ampiezza degli angoli; possiamo quindi trascurare la loro posizione nel piano, e per comodità studieremo solo angoli in una determinata posizione: aventi il vertice (O) nel centro della circonferenza e un lato (OA) sul semiasse positivo delle ascisse; il restante lato (OP) è libero di ruotare intorno all'origine, come rappresentato in figura 1.

^
Torna su

La misura degli angoli

In matematica e in fisica l'unità di misura più utilizzata per gli angoli sono i radianti: un radiante è l'ampiezza di un angolo al centro che sottende un arco di lunghezza uguale al raggio (1 rad = 57° circa).
Ricordiamo che la misura della circonferenza è: C = 2π·r, essendo π la costante di Archimede; quindi si ricava che il raggio sta 2π volte nella circonferenza. Facendo corrispondere ad ogni angolo al centro α il relativo arco AP sulla circonferenza [vedi figura sotto], possiamo affermare che:

In figura 1 l'arco è AP, indicato in rosso.

Di conseguenza un angolo giro è ampio 2π rad, un angolo piatto π rad, un angolo retto π ⁄ 2 rad; in generale se α° è la misura di un angolo in gradi e α_rad è la misura dello stesso angolo in radianti, valgono le formule:

[Trucchetto: In trigonometria è quindi utile pensare che pi-greco sia una costante che indichi 180°, piuttosto che il solito 3,14: anche se non è proprio corretto, aiuta a familiarizzare con i radianti.]

Facendo sempre riferimento alla figura 1, l'ampiezza di un angolo è considerata positiva se, partendo dal lato fisso (OA) raggiungiamo il lato mobile (OP) in senso anti-orario, ed è considerata negativa se ci muoviamo in senso orario. Quindi uno stesso angolo si può considerare negativo o positivo a seconda di come raggiungiamo il lato OP.

Graficamente ogni angolo può essere ricondotto ad un angolo compreso tra 0 e 2π: ad esempio 7π coincide con π (abbiamo solo fatto tre giri in più), lo stesso 2π coincide con 0; quindi d'ora in avanti per comodità considereremo solo angoli α tali che: 0 ≤ α < 2π.

« Non per la scuola, ma per la vita s'impara »

Seneca

^
Torna su

Sotto-sezioni di Trigonometria

La sezione di Trigonometria contiene pagine che descrivono e spiegano i seguenti argomenti:

Funzioni - Formulario - Triangoli