Triangoli rettangoli - Triangoli e circonferenza - Triangoli qualunque

★ ★ ☆

<<< Precedente   -   Successivo >>>

Triangoli rettangoli
Teoremi

Triangoli rettangoli

Le funzioni goniometriche sono state definite in due modi: partendo dalle relazioni tra i lati di un triangolo rettangolo, oppure partendo dalle coordinate di un punto sulla circonferenza goniometrica; le die definizioni sono equivalenti, infatti su tale circonferenza si possono individuare triangoli rettangoli, dai quali abbiamo ricavato tutte le proprietà e le relazioni viste.

In particolare possiamo riprendere la prima definizione, e scrivere in modo più efficace le relazioni tra i lati di un triangolo rettangolo generico.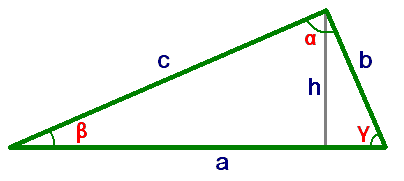
Con riferimento alla figura 1, in cui α = π ⁄ 2 (ossia 90°, l'angolo retto), sappiamo che:

• il seno di un angolo acuto è il rapporto tra il cateto opposto all'angolo e l'ipotenusa:
  sen (β) = b ⁄ a   e   sen (γ) = c ⁄ a
• il coseno di un angolo acuto è il rapporto tra il cateto adiacente all'angolo e l'ipotenusa:
  cos (β) = c ⁄ a   e   cos (γ) = b ⁄ a.

^
Torna su

Teoremi

Da queste definizioni possiamo ricavare tutte le relazioni tra i lati e gli angoli, utilizzando le funzioni seno, coseno, tangente, cotangente; in particolar modo:

Ricordiamo che l'altezza relativa all'ipotenusa divide un triangolo rettangolo in due rettangolini simili al triangolo inizale. Per cui possiamo applicare anche a questi triangoli i risultati precedenti, in particolare:

Questi risultati sono molto importanti in quanto collegano le proprietà degli angoli (viste nelle altre pagine) alle proprietà dei triangoli rettangoli, in particolare a semplici rapporti tra lati. Inoltre qualunque poligono può esser scomposto in triangoli rettangoli, di conseguenza molte proprietà dei poligoni sono riconducibili ai triangoli rettangoli.

^
Torna su

<<< Precedente   -   Successivo >>>