Triangoli rettangoli - Triangoli e circonferenza - Triangoli qualunque

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Triangoli & circonferenza
Altri teoremi sulla circonferenza

Triangoli & circonferenza

Anche la circonferenza è strettamente collegata ai triangoli rettangoli, in quanto ricordiamo che:

ogni triangolo rettangolo inscritto in una semi-circonferenza è rettangolo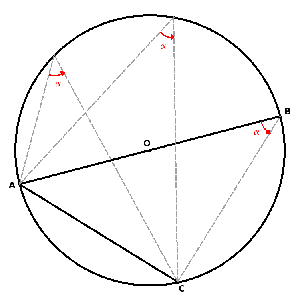

dove con inscritto in una semi-circonferenza intendiamo avente l'ipotenusa coincidente con il diametro del cerchio e il vertice dell'angolo retto sulla semi-circonferenza.

Collegato a questi risultati c'è un importante teorema.
Con riferimento alla figura 2, consideriamo il triangolo ABC: esso è rettangolo, avendo l'ipotenusa AB coincidente con il diametro, per cui:

AC = AB · sen(α)

in quanto l'angolo acuto α è opposto al cateto AC; inoltre α è un angolo alla circonferenza che insiste su AC, e tutti gli angoli alla circonferenza che insistono su AC sono congruenti tra loro, come mostrato in figura; per cui questa formula vale per ogni angolo α che scegliamo.

Possiamo quindi dire che:

Da questo risultato si ottengono molte proprietà relative alla circonferenza e risultati importanti, eccone alcuni (per dimostrare questi risultati è sufficiente applicare opportunamente le similitudini tra triangoli).

Esempio 2. Quanto vale il lato di un quadrato ABCD inscritto in una circonferenza di raggio 50cm? Dati. raggio:   r = 50cm lato:   ℓ = incognita Svolgimento. Per calcolare il lato del quadrato, dobbiamo vederlo come una corda della circonferenza; consideriamo ad esempio il lato AB. Inoltre ci serve sapere l'angolo α che insiste sul lato; per trovare α è sufficiente collegare gli estremi del lato AB ad un qualunque punto della circonferenza; per comodità conviene collegarlo ad uno degli altri due vertici del quadrato,ad esempio C, come indicato in figora 3. Quindi l'angolo α corrisponde ad AĈB, che è la metà dell'angolo retto DĈB, quindi: α = π/4 Applichiamo il teorema della corda, per calcolare la lunghezza ℓ della corda AB: ℓ = 2r · sen (α) ℓ = 2 · 50cm · sen (π/4) ℓ = 100cm · √2/2 ℓ = 50√2cm Conclusione: il lato del quadrato è lungo 50√2cm.

^
Torna su

Altri teoremi sulla circonferenza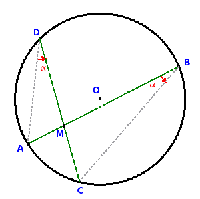

Consideriamo una circonferenza Γ (gamma) e due corde AB e CD aventi un punto in comune M, i segmenti in cui sono divise rispettano una proporzione; infatti, con riferimento alla figura 4, possiamo osservare che i triangoli ADM e BCM sono simili, in quanto hanno tutti gli angoli congruenti (una coppia è opposta al vertice, le altre sono coppie di angoli alla circonferenza dello stesso arco); quindi si ottiene una proporzione tra i lati.

Formalizzando, giungiamo al seguente teorema:

Da cui segue anche un'altra importante proprietà: infatti, applicando la proprietà fondamentale delle proporzioni, si ottiene che:

AM · MB = CM · MD

Sia P un punto esterno alla circonferenza Γ e siano r e s due rette secanti la circonferenza; siano A e B i punti d'intersezione tra r e Γ, siano C e D quelli tra s e Γ. Allora i segmenti PA, PC, PD, PB sono in proporzione, ovvero:

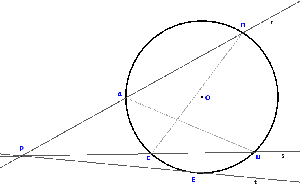
Infatti, consideriamo i triangoli PBC e PAD della figura 5: essi hanno tutti e tre gli angoli congruenti (P in comune, B = C in quanto entrambi insistono sull'arco AC, gli altri per differenza) perciò sono simili.

Di conseguenza il rapporto tra i lati è costante, quindi: PA ∶ PC = PD ∶ PB, come afferma il teorema.

Possiamo considerare anche i segmenti PA, PC, CD, AB, anch'essi in proporzione per la regola dello scomporre delle proporzioni.

Nel caso in cui al posto di una secante vi sia una tangente, si ottiene un risultato simile: se per esempio la retta t (passante per P) è tangente alla circonferenza Γ nel punto E, allora i triangoli PBE e PEA sono simili, ottenendo quindi una proporzione tra le lunghezze dei 3 segmenti PA, PB e PE, dove quest'ultimo è medio proporzionale tra gli altri due, ovvero:

Come conseguenza di questo teorema, abbiamo che:

PE = √PA · PB

^
Torna su

<<< Precedente   -   Successivo >>>