★ ☆ ☆

CONTENUTO DELLA PAGINA
La Geometria Analitica
Il piano cartesiano
Sotto-sezioni

La Geometria Analitica

La Geometria Analitica fa parte dell'analisi matematica e studia la geometria in modo appunto analitico, ossia descrive le possibili relazioni tra le figure geometriche (come punti, rette, poligoni, curve e superfici) e strumenti algebrici (come ad esempio espressioni, equazioni, disequazioni e sistemi).

Questo approccio analitico della geometria è complementare ad uno studio sintetico più tradizionale, nel quale si confrontano le proprietè grafiche delle figure, tramite relazioni di congruenza o di similitudine; per sapere di più sulla geometria sintetica tradizionale visita questa sezione.

Nello studio della geometria analitica, ogni elemento geometrico è collegato ad elementi algebrici; ad esempio il piano, concetto primitivo della geometria, viene arricchito di un sistema di riferimento cartesiano, ogni punto è associato a determinate coordinate numeriche, ogni luogo geometrico può esser identificato da oppurtune equazioni o disequazioni.

Ma andiamo in ordine, iniziamo con il descrivere l'ambiente di lavoro, ossia il piano cartesiano.

Il piano cartesiano

Un elemento di partenza per lo studio della geometria analitica è, come abbiamo detto, il piano cartesiano:

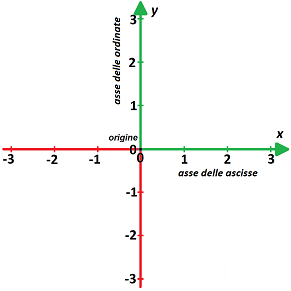
Spieghiamo meglio questa definizione, aiutandoci con la figura 1, in cui è riportato un comune piano cartesiano (anche se un po' colorato): sono disegnate due rette perpendicolari, una orizzontale e una verticale, che si incontrano nel punto O (da qui il termine "orto" = dritto, retto); le due rette sono orientate, in quanto hanno un verso di percorrenza indicato dalla punta della freccia, graduate, e l'unità di misura fissata in una retta è uguale all'unità di misura fissata nell'altra retta (da qui il termine "normale" = che entrambe seguono una norma, una regola comune).

La retta orizzontale è chiamata asse delle ascisse, o asse x; la retta verticale asse delle ordinate, o asse y.

Esiste una corrispondenza biunivoca tra i numeri reali e i punti su una retta, per cui possiamo fissare su ognuno di questi assi il punto che corrisponde allo zero, quello che corrisponde all'uno, quello che corrisponde a due e così via… in particolare, per convenzione, il punto di intersezione tra i due assi (il punto O) viene chiamato origine degli assi e si pone in corrispondenza dello zero in ciascuna retta: le due rette hanno l'origine in comune, lo stesso zero.

I punti sull'asse delle x nel semiasse di destra (colore verde) corrispondono a numeri positivi, mentre i negativi corrispondono ai punti nel semiasse di sinistra (colore rosso); analogamente l'asse delle y ha valori positivi in alto (colore verde) e negativi in basso (colore rosso); per non confonderci, le semirette corrispondenti ai numeri positivi dei due assi sono caratterizzate dalla freccia alla loro fine, cosa che non si deve mettere nei semiassi negativi!

« La matematica è l'alfabeto con il quale Dio ha scritto il mondo »

Pitagora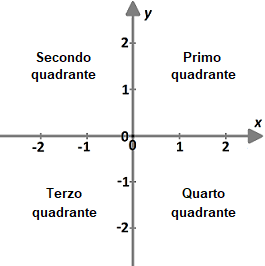

Le 4 zone in cui viene diviso il piano dagli assi cartesiani sono chiamati quadranti:

1. il primo quadrante è quello in alto a destra;
2. il secondo quadrante è in alto a sinistra;
3. il terzo quadrante è in basso a sinistra;
4. il quarto quadrante è in basso a destra.

Ricordiamo che in matematica e in fisica, il verso di rotazione standard è quello anti-orario, per cui fissato il primo quadrante, gli altri si contano seguendo questo ordine, come indicato in figura 2.

^
Torna su

Sotto-sezioni di Geometria Analitica

La sezione di Geometria Analitica contiene pagine che descrivono e spiegano i seguenti argomenti:

Punti e rette - La parabola - La circonferenza - L'ellisse - L'iperbole - Coniche in generale - Trasformazioni