Equazione canonica - Proprietà principali - Trasformazioni

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Definizione
L'ellisse come conica
Caratteristiche dell'ellisse

Definizione

L'ellisse è una curva piana chiusa, che di definisce nel seguente modo:

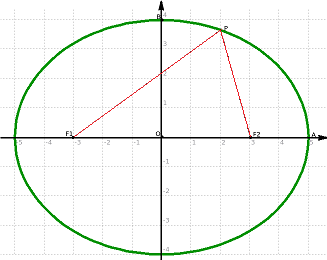
In queste pagine consideriamo solo un caso particolare di ellissi: quelle aventi i fuochi sull'asse delle x, simmetrici rispetto all'origine (vedi figura 1).

Poniamo quindi:   F₁ = (−c, 0)   e   F₂ = (c, 0)

con c reale positivo; il caso c = 0 lo possiamo anche accettare, ma è un caso limite, in quanto l'ellisse degenera in una circonferenza.
Supponiamo che la somma costante delle distanze valga 2a, con a > c, e consideriamo un generico punto P = (x, y) dell'ellisse [vedi figura 1].

Applicando la definizione otteniamo la seguente equazione:

PF₁ + PF₂ = 2a

Svolgendo i calcoli:

√(x + c)² + y² + √(x − c)² + y² = 2a

√(x + c)² + y² = 2a − √(x − c)² + y²

(x + c)² + y² = 4a² + (x − c)² + y² − 4a√(x − c)² + y²

4cx − 4a² = − 4a√(x − c)² + y²

a² − cx = a√(x − c)² + y²

a⁴ + c²x² − 2a²cx = a²x² + a²c² − 2a²cx + a²y²

(a² − c²)x² + a²y² = a²(a² − c²)

essendo a > c, possiamo porre: a² − c² = b²
Sotto tali ipotesi l'equazione dell'ellisse si scrive nella forma:

b²x² + a²y² = a²b²

con a e b coefficienti reali positivi, a > b. Quest'ultima equazione è la forma canonica di un'ellisse.

Può anche capitare che sia a < b; in tale caso vuol dire che:

• l'ellisse ha i fuochi sull'asse y, anziché sull'asse x;
• le coordinate dei fuochi sono quindi F₁ = (0, −c) e F₂ = (0, c);
• b² = a² + c².

Osservazione: la circonferenza e la parabola sono casi particolari di ellisse: la circonferenza ha i fuochi coincidenti nel centro: C = F₁ = F₂; per cui è costante la distanza di P da C, come afferma la definizione della circonferenza; la parabola è un caso ancora più particolare di ellisse, in quanto ha uno dei due fuochi a "distanza infinita" (quindi si può vedere solo una parte dell'ellisse, e solo un fuoco).

^
Torna su

L'ellisse come conica

Geometricamente l'ellisse è una sezione conica ottenuta intersecando la superficie di un cono circolare con un piano "quasi" perpendicolare all'asse del cono. Per la precisione, supponendo che l'asse del cono sia verticale, l'inclinazione del piano non può esser uguale o superiore all'inclinazione di una qualunque generatrice del cono.
Nel caso in cui il piano passa per il vertice l'ellisse degenera in un punto.

Ricordiamo che una conica può esser definita come luogo nel seguente modo:

F è detto fuoco, d è detta direttrice e il rapporto e = PF / PH è chiamato eccentricità; essendo un rapporto tra grandezze geometriche, l'eccentricità è un valore non negativo.

Nel caso in cui e < 1 la conica è una 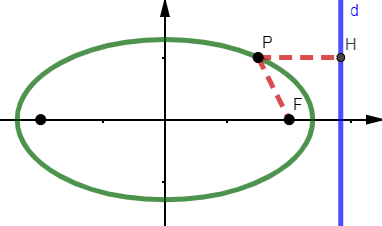ellisse.

Fissiamo a (semiasse maggiore) e c (semidistanza focale) con 0 < c < a; il caso c = 0 si ha quando l'ellisse diventa una circonferenza, ma ora lo dobbiamo escludere per poter svolgere i calcoli. Quindi poniamo:

• F = (c, 0) il fuoco positivo dell'ellisse
• d: x = a² ⁄ c
• e = c ⁄ a < 1

Cerchiamo tutti e soli i punti P = (x, y) che verificano la definizione della conica. Sia H = (a²/c, y) la proiezione di P su d (vedi figura 2), allora:

PF = √(x − c)² + y²     PH = | x − a² ⁄ c |

Quindi:

PF = PH · e

√(x − c)² + y² = | x − a² ⁄ c | · (c ⁄ a)

a · √(x − c)² + y² = | cx − a² |

a² · (x² − 2cx + c² + y²) = c²x² − 2a²cx + a⁴

a²x² + a²c² + a² y² = c²x² + a⁴

(a² − c²)x² + a²y² = a²(a² − c²)

Osserviamo che i passaggi precedenti sono equivalenti per ogni conica, in quanto l'unica differenza è il valore di e, non utilizzato.
Dal momento che e < 1, allora a > c e quindi la quantità a² − c² è positiva. Possiamo quindi porre:

b² = a² − c²

Successivamente dividiamo per a²b² riottienendo la forma:

In conclusione osserviamo che siamo tornati ai passaggi della precedente definizione, dunque le due definizioni sono equivalenti.

^
Torna su

Caratteristiche dell'ellisse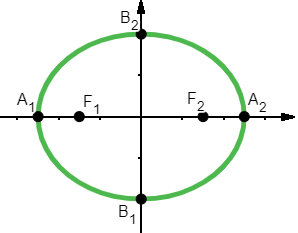

♦ L'ellisse, come abbiamo visto, possiede due fuochi, F₁ ed F₂; la loro distanza è chiamata asse focale e vale 2c, indipendentemente da dove si trovano i fuochi.

♦ Essendo una conica, l'ellisse, possiede anche due rette direttrici (una per ciascun fuoco); tali direttrici sono rette esterne all'ellisse, perpendicolari all'asse focale; nel nostro caso, in un'ellisse con centro nell'origine e fuochi sull'asse x, essi valgono:

e ciascuna coppia fuoco-direttrice può esser utilizzata per generare l'ellisse.

♦ Esistono sempre 4 punti di intersezioni tra l'ellisse e gli assi, detti vertici, come indicato in figura 3

Nel caso semplice di un'ellisse con centro nell'origine essi hanno coordinate:

♦ L'ellisse possiede due assi di simmetria, che sono corde che uniscono i vertici opposti:

• l'asse maggiore è quello su cui si trovano i fuochi;
• l'asse minore è quello su cui non si trovano i fuochi.

Se l'ellisse ha centro nell'origine, i due assi di simmetria si trovano sugli assi cartesiani:

• l'asse A₁A₂ si trova sull'asse x e misura 2a;
• l'asse B₁B₂ si trova sull'asse y e misura 2b.

♦ L'eccentricità (e) di un ellisse è data dal rapporto:

nel nostro caso, in un'ellisse con centro nell'origine e fuochi sull'asse x, l'eccentricità vale:

e = c ⁄ a

e il suo valore è sempre compreso tra 0 e 1.

^
Torna su

<<< Precedente   -   Successivo >>>