Equazione - Proprietà - Fasci

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Definizione
Equazione generale
Circonferenza e funzioni

Definizione

Geometricamente la circonferenza è una sezione conica ottenuta intersecando la superficie di un cono circolare con un piano perpendicolare all'asse del cono. Tale intersezione diventa banale se il piano passa per il vertice del cono: la circonferenza degenera in un punto.

Il caso più semplice di circonferenza è quella avente come centro l'origine degli assi e raggio 1 (vedi figura 1); applicando il teorema di Pitagora per un generico punto P(x₀, y₀), abbiamo che:

x₀² + y₀² = 1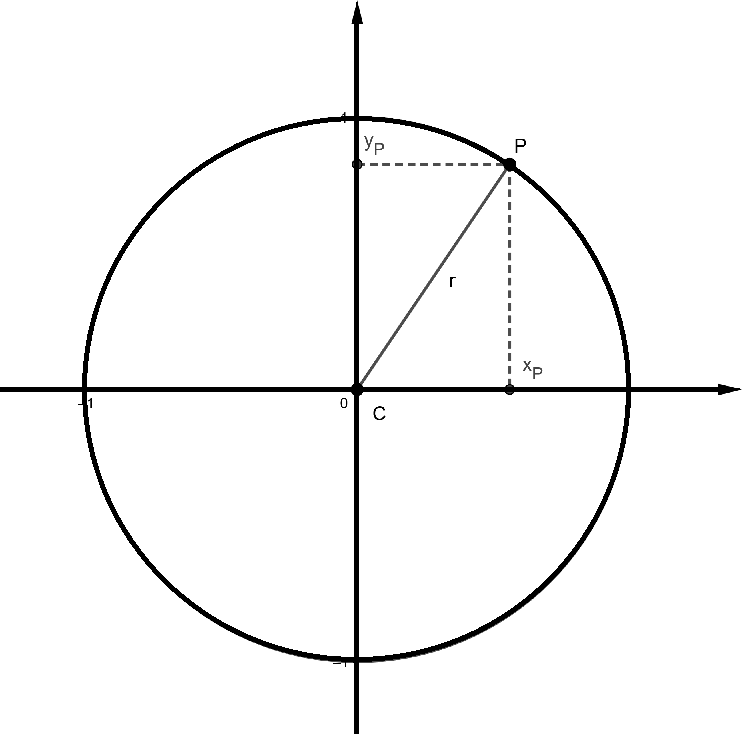

Quindi l'equazione di questa circonferenza è:

x² + y² − 1 = 0

In generale l'equazione di una circonferenza avente come centro l'origine e raggio r qualunque è:

^
Torna su

Equazione generale

Per arrivare all'equazione generale della circonferenza, occorre imporre la condizione data dalla definizione: la distanza di un qualunque punto dal centro deve essere uguale al raggio.
Sia Ω(α, β) il centro, e sia r la lunghezza del raggio; applicando la formula per la distanza tra due punti si ottiene:

√(x − α)² + (y − β)² = r

svolgendo i calcoli:

(x − α)² + (y − β)² = r²

x² − 2αx + α² + y² − 2βy + β² − r² = 0

e ponendo:

• a = − 2α
• b = − 2β
• c = α² + β² − r²

otteniamo l'equazione canonica della circonferenza:

Dalla formula generale, e dalla definizione di a, b, c, ricaviamo le formule per le caratteristiche della circonferenza:

Osservazione: la circonferenza è un caso particolare di ellisse avente i semiassi uguali tra loro, di lunghezza r:

a = b = r

La sua eccentricità quindi vale:

e = √(1 − r/r) = 0.

Può esser vista quindi come una conica avente la direttrice infinitamente lontana dal fuoco e dalla conica stessa; questo comporta tra l'altro che la distanza dal fuoco (che diventa il centro), essendo infinitamente inferiore, può esser assunta costante (e diventa il raggio).
Di conseguenza però non è più possibile usare l'equazione generica di conica per descrivere la circonferenza.

^
Torna su

Circonferenza e funzioni

La circonferenza è una curva chiusa; è possibile rappresentarla sul piano solo se vale la seguente condizione:

a² + b² − 4c ≥ 0

che corrisponde ad imporre che il raggio abbia un valore reale; tale condizione si può riscrivere:

a² + b² ≥ 4c

L'equazione della circonferenza non può essere messa in forma esplicita; infatti se ad esempio proviamo ad esplicitare la y (come per la retta) otteniamo:

(y − β)² = r² − (x − α)²

Per togliere il quadrato dobbiamo effettuare un'estrazione a radice in ambo i membri, ponendo la condizione:

α − r < x < α + r

Inoltre è necessario porre il ± davanti alla radice; otteniamo quindi:

y − β = ± √ r² − (x − α)²

y = β ± √ r² − (x − α)²

Scritta in questo modo, la circonferenza non è più una curva unica, ma è vista come l'unione di due funzioni: ogni funzione reppresenta una semicirconferenza, una superiore e una inferiore:

𝒞₁ :   y = β + √ r² − (x − α)²   con y > β

𝒞₂ :   y = β − √ r² − (x − α)²   con y < β

Possiamo sostituire i coefficienti a, b, c:

𝒞₁ :   y = − b/2 + √− x² − ax + (b²/4) − c

𝒞₂ :   y = − b/2 − √− x² − ax + (b²/4) − c

^
Torna su

<<< Precedente   -   Successivo >>>