Sito del prof Caroselli - La circonferenza

Inizio

News

CIRCONFERENZA

Info

Equazione - Proprietà - Fasci

★ ★ ☆

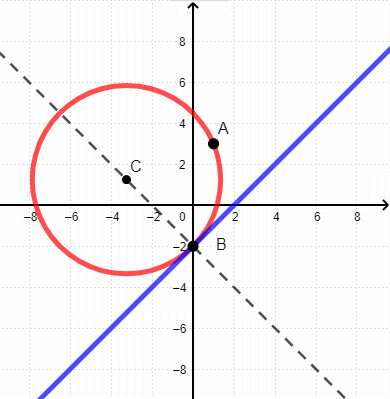
<<< Precedente - Successivo >>>

Circonferenza e rette
Circonferenza come conica

Circonferenza e rette

Una circonferenza e una retta possono avere fino a due punti d'intersezione; tali punti si possono trovare risolvendo il sistema di II grado tra l'equazione della retta e quella della circonferenza; l'esistenza di questi punti si verifica studiando il discriminate dell'equazione risolutrice:

se il Δ > 0, la distanza della retta dal centro è minore del raggio e la retta è secante la circonferenza: si hanno deu punti d'intersezione distinti;
se il Δ = 0, la distanza della retta dal centro è uguale al raggio e la retta è tangente alla circonferenza in un punto (due punti d'intersezione coincidenti);
se il Δ < 0, la distanza della retta dal centro è maggiore del raggio e la retta è esterna alla circonferenza: non si hanno punti d'intersezione;

quindi una generica retta tangente alla circonferenza si trova imponendo: Δ = 0.

Inoltre, ricordando le proprietà geometriche della circonferenza, dato un fascio di rette passanti per un punto P(x₀ y₀), avente equazione:

y − y₀ = m (x − x₀)

per determinare l'equazione della retta del fascio tangente alla circonferenza, si può determinare il coefficiente angolare m in modo che la retta abbia distanza dal centro di un valore uguale al raggio.

Oppure, se il punto P(x₀, y₀) è il punto di tangenza, si può applicare la condizione che la retta sia perpendicolare al raggio OP.

Infine si può usare la formula di sdoppiamento:

Formula di sdoppiamento

𝓉 : x·x₀ + y·y₀ + ½ a(x + x₀) + ½ b(y + y₀) + c = 0

Esempio 3. Determiniamo l'equazione della retta passante per il punto P(− 1; 3) e tangente alla circonferenza di equazione:

x² + y² + 2x + 6y + 4 = 0

Svolgimento. La retta passante per P appartiene al fascio di equazione:

y − y₀ = m (x − x₀) ∨ x = x₀

essendo x₀ ed y₀ le coordinate di P, ed m il coefficiente da trovare

y − 3 = m (x + 1) ∨ x = − 1

Il caso x = − 1 corrisponde alla retta verticale del fascio, e possiamo verificare subito se essa è tangente o meno alla circonferenza, mettendo a sistema le due equazioni:

⎧ x² + y² + 2x + 6y + 4 = 0
⎨
⎩ x = − 1

Sostituiamo la seconda equazione all'interno della prima, e svolgiamo i calcoli:

(−1)² + y² + 2(−1) + 6y + 4 = 0

1 + y² − 2 + 6y + 4 = 0

y² + 6y + 3 = 0

Il delta di questa equazione vale:

Δ = b² − 4ac =

= (6)² − 4(1)(3) =

= 36 − 12 = 24

Essendo un numero positivo, tale retta è secante, quindi non è una delle tangenti che cerchiamo. Passiamo quindi al caso generico:

y − 3 = m (x + 1)

y = m (x + 1) + 3

y = mx + m + 3

E studiamo il sistema:

⎧ x² + y² + 2x + 6y + 4 = 0
⎨
⎩ y = mx + m + 3

Anche in questo caso sostituiamo la seconda equazione all'interno della prima, e svolgiamo i calcoli:

x² + (mx + m + 3)² + 2x + 6(mx + m + 3) + 4 = 0

x² + m²x² + m² + 9 + 2m²x + 6m + 6mx + 2x + 6mx + 6m + 18 + 4 = 0

(1 + m²)x² + (2m² + 12m + 2)x + m² + 12m + 31 = 0

(1 + m²)x² + 2(m² + 6m + 1)x + m² + 12m + 31 = 0

Come prima, calcoliamo il delta dell'equazione risolutiva, con la differenza che qui i termini contengono il coefficiente m.
In questo caso per comodità calcoliamo il Δ/4, anziché il Δ completo:

Δ/4 = (b/2)² − ac =

= (m² + 6m + 1)² − (1 + m²)(m² + 12m + 31) =

= m⁴ + 36m² + 1 + 12m³ + 12m + 2m² +

− (m² + 12m + 31 + m⁴ + 12m³ + 31m²) =

= m⁴ + 36m² + 1 + 12m³ + 12m + 2m² +

− m² − 12m − 31 − m⁴ − 12m³ − 31m² =

= 6m² − 30

Per trovare le rette tangenti, dobbiamo porre il delta (in questo caso Δ/4) uguale a zero e trovare m:

6m² − 30 = 0

6m² = 30

m² = 5

m = ± √5

Abbiamo trovato due possibili valori di m, entrambi accettabili, quindi vi sono due rette passanti per P, entrambe tangenti alla circonferenza.

Conclusione: le rette tangenti alla circonferenza hanno equazione:

y = ± √5 (x + 1) + 3

^
Torna su

Condizioni per determinare l'equazione di una circonferenza

L'equazione di una circonferenza può esser determinata qualora si conoscano alcune sue proprietà: normalmente, qualora non si voglia determinare l'equazione partendo da alcune sue proprietà, si parte dalconsiderare l'equazione canonica:

x² + y² + ax + by + c = 0

avendo come obiettivo il trovare i valori numerici dei parametri a, b, c. Tali parametri si possono ottenere mettendo a sistema equazioni che si ricavano dai dati del problema.

Ecco alcuni esempi di condizioni sufficienti per determinare l'equazione di una circonferenza:

si conosce un punto appartenente alla circonferenza: si applica la condizione di appartenenza, sostituendo le coordinate del punto nell'equazione canonica;
si conoscono le coordinate del centro: il centro ci fornisce 2 condizioni, che possiamo utilizzare per costruire il sistema:
- x del centro: uguagliamo la formula per la x del centro al valore noto;
- y del centro: uguagliamo la formula per la y del centro al valore noto;
si conosce la lunghezza del raggio: uguagliamo la formula per trovare il raggio al valore dell'equazione;
si conoscono il centro e un punto della circonferenza: con la distanza tra due punti si può calcolare la lunghezza del raggio;
si conoscono gli estremi del diametro: con la distanza tra due punti si può calcolare la lunghezza del diametro, che è il doppio del raggio; inoltre con la formula del punto medio si trovano le coodinate del centro;
si conosce una retta tangente: si pone la condizione di tangenza: in un sistema a parte, si confrontando l'equazione della retta e l'equazione canonica della circonferenza, e nell'equazione risultante si studia il delta, ponendolo uguale a zero;
si conosce una retta tangente e il centro: si calcola il raggio, con la formula distanza punto-retta;
si conosce una retta tangente e il punto di tangenza: si calcola la retta che passa per il centro, come retta perpendicolare alla tangente, passante per il punto di tangenza; quindi si applica la condizione di appartenenza, sostituendo le formule del centro nell'equazione della retta trovata.

Osservazione: Per applicare le condizioni di appartenenza o di tangenza non è necessario conoscere i valori numerici degli elementi coinvolti: in caso non si conoscano, si usano le formule o le lettere generali.

Esempio 4. Determiniamo l'equazione della circonferenza passante per il punto A(1; 3) e tangente in B (0; − 2) alla retta t di equazione:

t : y = x − 2.

Svolgimento. Il nostro obiettivo è trovare il valore dei coefficienti a, b, c presenti nell'equazione canoca:

x² + y² + ax + by + c = 0

Studiamo le condizioni date dal testo, per ricavare le equazioni da inserire nel sistema.

Prima condizione: passaggio per il punto A: sostituiamo le coordinate di A all'interno dell'equazione canonica:

(1)² + (3)² + a(1) + b(3) + c = 0

1 + 9 + a + 3b + c = 0

a + 3b + c + 10 = 0

Seconda condizione: passaggio per il punto B: sostituiamo le coordinate di B all'interno dell'equazione canonica:

(0)² + (− 2)² + a(0) + b(− 2) + c = 0

0 + 4 + 0 − 2b + c = 0

− 2b + c + 4 = 0

Terza condizione: tangenza tra la retta t e la circonferenza: non avendo né il centro né il raggio, non possiamo usare la regola della distanza centro-punto = raggio; tuttavia possiamo usare la regola che il raggio è perpendicolare alla retta nel punto di tangenza, e quindi che il centro deve appartenere alla perpendicolare a t in B (in alternativa possiamo studiare il sistema retta-circonferenza e porre Δ = 0).
Per prima cosa calcoliamo la perpendicolare a t in B, tramite la formula della retta passante per un punto, mettendo il coefficiente angolare anti-reciproco di t, ossia −1.

y − y₀ = m⊥ (x − x₀)

y − (− 2) = −1 (x − 0)

y + 2 = − x

Mettendo in forma implicita questa retta:

x + y + 2 = 0

Ora sostituiamo le coordinate (generiche) del centro in questa equazione:

(−a/2) + (−b/2) + 2 = 0

− a/2 − b/2 + 2 = 0

− a − b + 4 = 0

A questo punto costruiamo il sistema con le tre equazioni trovate.

⎧ a + 3b + c + 10 = 0
⎨ − 2b + c + 4 = 0
⎩ − a − b + 4 = 0

Per risolvere questo sistema, dobbiamo esplicitare due lettere in funzione della terza; osservando le equazioni, notiamo che la seconda e la terza equazione possono esser esplicitate in funzione di b:

⎧ a + 3b + c + 10 = 0
⎨ c = 2b − 4
⎩ a = − b + 4

A questo punto sostituiamo la seconda e la terza equazione all'interno della prima, e svolgiamo i calcoli:

(− b + 4) + 3b + (2b − 4) + 10 = 0

− b + 4 + 3b + 2b − 4 + 10 = 0

4b + 10 = 0

4b = − 10

b = − 5/2

Ora è sufficiente risostituire il valore di b trovato per determinare a e c:

a = − b + 4 ⇒ a = −(−5/2) + 4 = 13/2

c = 2b − 4 ⇒ c = 2(−5/2) − 4 = − 9

Abbiamo risolto il sistema e trovato i tre coefficienti da inserire nell'equazione.

⎧ b = − 5/2
⎨ c = − 9
⎩ a = + 13/2