Relazioni fondamentali - Angoli associati - Formule goniometriche

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
1ª relazione fondamentale
2ª relazione fondamentale
Altre relazioni fondamentali

Attenzione: può accadere che alcuni simboli non siano visualizzati correttamente, leggi le info alla sezione compatibilità.

In queste pagine è presente un elenco delle proprietà principali delle funzioni gonometriche e dei risultati più utili nella risoluzione dei problemi trigonometrici.
Puoi anche consultare la tabella con i valori delle funzioni per gli angoli più importanti per verificare le diverse formule descritte qui di seguito.

1ª relazione fondamentale

In questa pagina sono elencate le identità (o relazioni) fondamentali della goniometria, che si ricavano applicando i teoremi sui triangoli rettangoli alla circonferenza goniometrica. Per prima cosa studiamo la relazione che lega seno e coseno di uno stesso angolo:

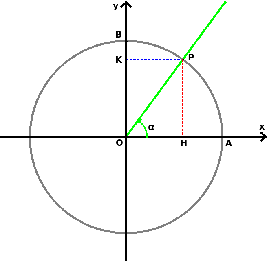
Questa relazione è la formula più importante di tutta la goniometria, in quanto chiarisce che il coseno e il seno di un angolo non sono coordinate di un punto qualunque del piano, ma dei punti appartententi alla circonferenza goniometrica (x² + y² = 1).

Questa relazione ha una dimostrazione immediata.
Infatti, guardando la figura 1, ci si accorge che il coseno e il seno sono i cateti di un triangolo rettangolo (ad esempio OH è il coseno e PH è il seno) e l'ipotenusa di tale triangolo è il raggio della circonferenza goniometrica, che vale 1.
Per cui, per il teorema di Pitagora, la somma dei quadrati delle lunghezze dei cateti è uguale al quadrato della lunghezza dell'ipotenusa, ovvero:

(cos α)² + (sen α)² = (1)²

Ossia la prima identità.

Da questa relazione possiamo ricavare le formule inverse, che ci permettono di passare dal seno al coseno e viceversa, a patto di conoscere in quale quadrante ci troviamo: infatti spesso ad un valore del seno corrispondono due valori del coseno e anche ad un valore del coseno corrispondono due valori del seno.

cos² (α) = 1 − sen² (α)

sen² (α) = 1 − cos² (α)

Da cui, facendo la radice, si ottiene:

^
Torna su

2ª relazione fondamentale

Possiamo studiare anche studiare la relazione che esiste tra la tangente, il seno e il coseno di uno stesso angolo:

Questa relazione di fatto ci permette di calcolare la tangente, conoscendo il seno e il coseno dell'angolo: nella pratica è molto più utile conoscere la tangente di un angolo che conoscere le altre funzioni, in quanto con la tangente abbiamo informazioni sull'inclinazione dell'angolo.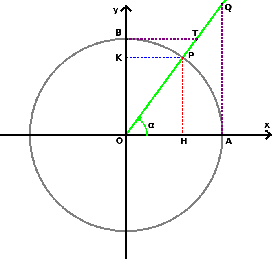

La dimostrazione di questa identità si basa sulle similitudini tra triangoli rettangoli.
Infatti, con riferimento alla figura 2, si può osservare che i triangoli rettangoli OPH e OQA sono simili in quanto hanno l'angolo α in comune; quindi possiamo scrivere la proporzione:

QA ∶ OA = PH ∶ OH

essendo QA la tangente di α OA il raggio, PH il seno e OH il coseno; perciò sostituendo si ottiene:

tan(α) ∶ 1 = sen(α) ∶ cos(α)

Ossia la seconda identità. Da ricordare che in una frazione il denominatore non può esser nullo per cui cos(α) ≠ 0, da cui: α ≠ π ⁄ 2 + kπ.

^
Torna su

Altre relazioni fondamentali

Le prime due relazione sono sufficienti a studiare le caratteristiche fondamentali di ogni angolo; tuttavia possiamo introdurre altre due relazioni che ci consentono di effettuare uno studio più completo.

La terza relazione ci permette di calcolare la cotangente di un angolo, conoscendo il coseno e il seno di un angolo.

La dimostrazione è simile a quella precedente: sfruttando la similitudine tra i triangoli rettangoli OBT e OKH (aventi un angolo acuto in comune), possiamo scrivere:

TB ∶ OB = PK ∶ OK

essendo TB la cotangente di α OB il raggio, PK il coseno e OK il seno; perciò sostituendo si ottiene:

cot(α) ∶ 1 = cos(α) ∶ sen(α)

Ossia la terza identità. Per le stesse limitazioni di prima, abbiamo questa volta che sen(α) ≠ 0, da cui: α ≠ kπ.

^
Torna su

Utile relazione che ci permette di compiere molte semplificazioni tra tangenti e cotangenti dello stesso angolo.

La dimostrazione è immediata, se si usano i risultati precendeti.

^
Torna su

<<< Precedente   -   Successivo >>>