Relazioni fondamentali - Angoli associati - Formule goniometriche

★ ★ ☆

<<< Precedente   -   Successivo >>>

Gli angoli associati
Angoli associati principali
Angoli associati secondari

Angoli associati

Ogni angolo, di qualunque ampiezza, può essere associato nel piano cartesiano ad un angolo del primo quadrante, ossia ad un angolo compreso tra 0 e π/2; questa associazione è legata a questioni di simmetria della circonferenza rispetto agli assi cartesiani.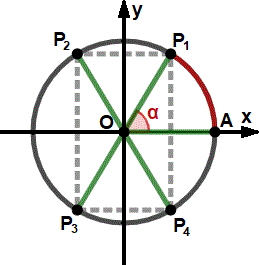

Infatti se un angolo si trova nel 2°, 3° o 4° quadrante, allora ci sta sicuramente un angolo nel 1° quadrante che ha una corrispondenza simmetrica con esso: ad esempio nella figura laterale (figura 3) l'arco AP₁ insiste sull'angolo AÔP₁, che ha ampiezza α; osserviamo che al punto P₁ corrispondono altri 3 punti, P₂, P₃ e P₄, rispettivamente nel 2°, nel 3° e nel 4° quadrante: ognuno di questi tre punti forma con A un angolo associato all'angolo α, infatti:

• dalla simmetria rispetto all'asse x otteneniamo l'angolo AÔP₄
• dalla simmetria rispetto all'asse y otteneniamo l'angolo AÔP₂
• dalla simmetria rispetto all'origine otteneniamo l'angolo AÔP₃

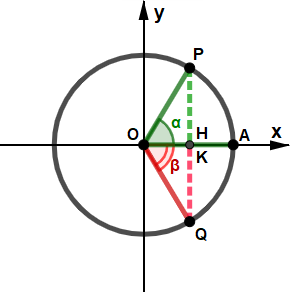
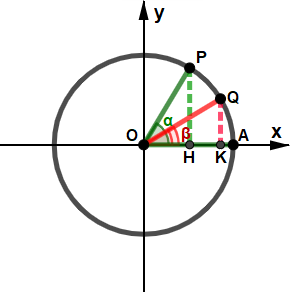
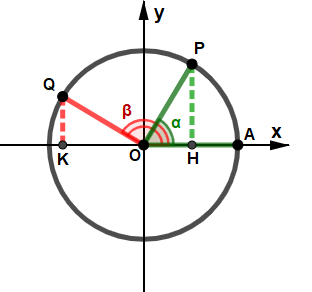
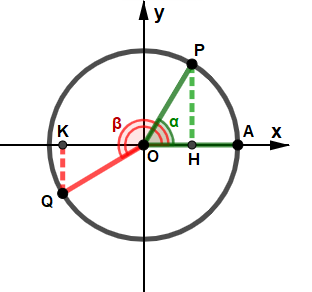
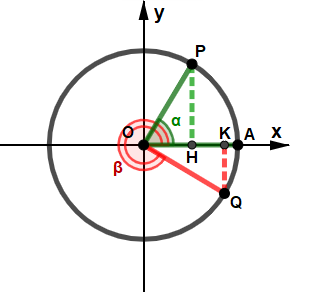
Possiamo ottenere punti simmetrici anche in altri modi, come ad esempio rispetto ad una delle bisettrici dei quadranti, o comporre più simmetria tra loro.

In questa pagina sono elencate le relazioni più comuni tra due angoli in base a possibili simmetrie; nelle figure che seguono il punto simmitrico a P è indicato con Q; l'angolo AÔQ, di ampiezza β (di colore rosso), è associato all'angolo AÔP, di ampiezza α (di colore verde); entrambi sono misurati in senso anti-orario, partendo da A.
Il coseno e il seno dell'angolo α sono rispettivamente le misure dei segmenti OH e PH; analogamente i segmenti OK e KQ sono rispettivamente il coseno e il seno dell'angolo β.

Angoli associati principali

Di seguito sono descritte i primi quattro casi che possono capitare: questi casi sono particolarmente facili, poiché gli angoli α e β hanno funzioni che conservano lo stesso valore assoluto, può cambiare in alcuni casi solo il segno.

⋄ Angoli opposti ⋄

Angoli la cui somma è l'angolo nullo.

Relazione: α + β = 0 β = −α Formule:   sen (β) = − sen (α)   cos (β) = cos (α)   tan (β) = − tan (α)   cot (β) = − cot (α)

Graficamente: I punti P e Q sono simmetrici rispetto all'asse x.

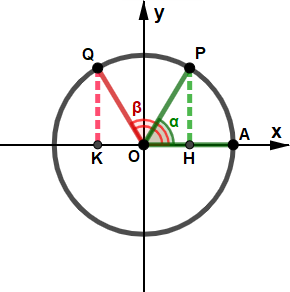
⋄ Angoli supplementari ⋄

Angoli la cui somma è l'angolo piatto.

Relazione: α + β = π β = π − α Formule:   sen (β) = sen (α)   cos (β) = − cos (α)   tan (β) = − tan (α)   cot (β) = − cot (α)

Graficamente: I punti P e Q sono simmetrici rispetto all'asse y.

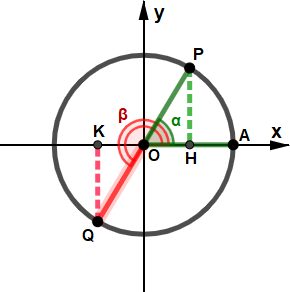
⋄ Angoli che differiscono di π ⋄

Relazione: β − α = π β = π + α Formule:   sen (β) = − sen (α)   cos (β) = − cos (α)   tan (β) = tan (α)   cot (β) = cot (α)

Graficamente: I punti P e Q sono simmetrici rispetto all'origine degli assi.

⋄ Angoli esplementari ⋄

Angoli la cui somma è l'angolo giro.

Relazione: α + β = 2π β = 2π − α Formule:   sen (β) = − sen (α)   cos (β) = cos (α)   tan (β) = − tan (α)   cot (β) = − cot (α)

Graficamente: I punti P e Q sono simmetrici rispetto all'asse x

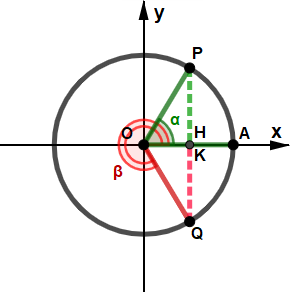
Osserviamo che quest'ultima situazione presenta le stesse formule del primo caso: se β è opposto ad α, oppure se è esplementare ad α le funzioni di β presentano comunque gli stessi valori; questo avviene perché le funzioni goniometriche sono periodiche, e ogni giro riassumono gli stessi valori.

^
Torna su

Angoli associati secondari

---

Oltre a queste relazioni, possiamo averne altre che coinvolgono l'angolo retto, come viene descritto nei casi seguenti. Quando nelle relazioni tra due angoli è coinvolto l'angolo retto, gli angoli α e β hanno funzioni che si scambiano tra loro i valori (il seno con il coseno e la tangente con la cotangente), inoltre in alcuni casi può cambiare anche il segno.

⋄ Angoli complementari ⋄

Angoli la cui somma è l'angolo retto.

Relazione: α + β = π/2 β = π/2 − α Formule:   sen (β) = cos (α)   cos (β) = sen (α)   tan (β) = cot (α)   cot (β) = tan (α)

Graficamente: I punti P e Q simmetrici sono rispetto alla bisettrice del I e III quadrante.

⋄ Angoli che differiscono di π/2 ⋄

Relazione: β − α = π/2 β = π/2 + α Formule:   sen (β) = cos (α)   cos (β) = − sen (α)   tan (β) = − cot (α)   cot (β) = − tan (α)

Graficamente: Simmetria composta: rispetto all'asse x e rispetto alla bisettrice del I e III quadrante.

⋄ Angoli la cui somma è 3⁄2 π ⋄

Relazione: α + β = 3⁄2 π β = 3⁄2 π − α Formule:   sen (β) = − cos (α)   cos (β) = − sen (α)   tan (β) = cot (α)   cot (β) = tan (α)

Graficamente: I punti P e Q simmetrici sono rispetto alla bisettrice del II e IV quadrante.

⋄ Angoli che differiscono di 3⁄2 π ⋄

Relazione: β − α = 3⁄2 π β = α + 3⁄2 π Formule:   sen (β) = − cos (α)   cos (β) = sen (α)   tan (β) = − cot (α)   cot (β) = − tan (α)

Graficamente: Simmetria composta: rispetto all'asse y e rispetto alla bisettrice del I e III quadrante.

^
Torna su

<<< Precedente   -   Successivo >>>