Equazione canonica - Proprietà principali - Altre proprietà

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Proprietà analitiche
Proprietà geometriche

Proprietà analitiche

♦ Una parabola di equazione y = ax² + bx + c, e una retta generica del piano possono avere al più 2 punti d'intersezione:

• se la retta è verticale, di equazione x = k si ha sempre uno e un solo punto d'intersezione, di coordinate:

  (k, ak² + bk + c)

• se la retta non è verticale, di equazione y = mx + q, può avere da 0 a 2 soluzioni, tante quante le soluzioni dell'equazione:

  ax² + (b − m)x + (c − q) = 0

  che si ottiene mettendo a sistema le equazioni della parabola e della retta; in particolare:
  1. se il sistema ammette due soluzioni distinte (Δ > 0) la retta è secante la parabola;
  2. se il sistema ammette due soluzioni coincidenti (Δ = 0) la retta è tangente alla parabola;
  3. se il sistema non ammette soluzioni reali (Δ < 0) la retta è esterna alla parabola.

♦ La parabola è utilizzata per calcolare in modo veloce il segno di un polinomio di II grado (ad esempio in una disequazione), mediante, per l'appunto, la regola della parabola.

♦ Se una retta è tangente alla parabola in un suo punto (x₀, y₀), allora avrà coefficiente angolare:

m = 2ax₀ + b

Per trovare l'equazione della retta si può quindi usare la formula:

y − y₀ = m · (x − x₀)

e sostituendo otteniamo:

In alternativa per determinare l'equazione di una retta tangente ad una parabola in un suo punto (x₀, y₀) si può utilizzare la formula di sdoppiamento, equivalente alla formula precedente:

^
Torna su

Proprietà geometriche

♦ Geometricamente la parabola è una sezione conica ottenuta intersecando la superficie di un cono circolare con un piano parallelo ad un lato del cono del cono.
Nel caso in cui il piano passa per il vertice la parabola degenera in una retta.

L'eccentricità di una parabola è 1: infatti, dato un punto P della parabola, l'eccentricità è il rapporto (costante in ogni conica) tra la distanza di P dal fuoco e la distanza di P dalla direttrice; tale rapporto deve essere 1, in quanto per la definizione di parabola le distanze sono uguali.

♦ La parabola ha un importante proprietà ottica: se dirigiamo dei raggi verso l'interno della parabola, diretti parallelamente all'asse, essi vengono riflessi in direzione del fuoco (vedi figura 4); viceversa i raggi emessi dal fuoco vengono riflessi dalla parabola in direzione parallela all'asse.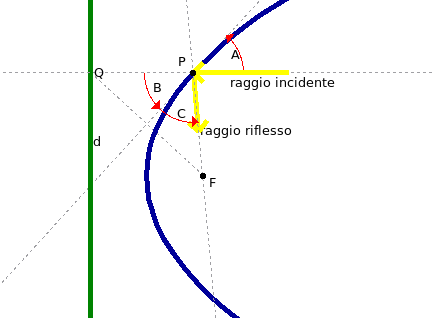

Infatti l'angolo d'incidenza e l'angolo di riflessione nel punto P, sono quelli generati con la retta tangente; l'angolo d'incidenza è l'angolo A, che è congruente all'angolo B (opposto al vertice), che a sua volta è congruente all'angolo C (poiché il punto P si trova sull'asse di FQ), che è l'angolo di riflessione.
Quindi il raggio segue esattamente questo percorso e viene riflesso proprio in tal modo, e tutti i raggi vanno a convergere nel fuoco della parabola. Analogamente tutti i raggi uscenti dal fuoco che incontrano la parabola vengono riflessi seguendo la direzione dell'asse della parabola.

♦ La regione di piano compresa tra la parabola ed una sua corda è chiamata segmento parabolico.
Un importante risultato, dovuto ad Archimede, legato al segmento parabolico è il:

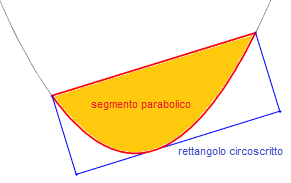
Se la corda è parallela alla direttrice della parabola il segmento parabolico è detto retto. Il teorema è molto importante nel caso di segmenti parabolici retti e ha applicazioni, oltre che in geometria, anche in analisi e in fisica.

Nella figura 5 è mostrato un esempio di segmento parabolico generico.

Data una parabola 𝒫 di equazione y = ax² + bx + c e due suoi punti A e B, possiamo tracciare la corda AB, che individua con la parabola un segmento parabolico.
L'area 𝒜 di tale segmento si può calcolare con la formula:

♦ Costruzione al computer di una parabola, utilizzando un qualunque software di geometria dinamica, come ad esempio Geogebra, Cabri o Kig:

1. si fissano il fuoco F e la direttrice d;
2. su d si fissano un punto T;
3. si traccia la perpedicolare a d passante per T;
4. si traccia l'asse del segmento TF;
5. il punto d'intersezione tra l'asse e la perpendicolare si chiama P;
6. si imposta il luogo dei punti P al variare di T;
7. il luogo creato è una parabola.

^
Torna su

<<< Precedente   -   Successivo >>>