|
★ ★ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
Carattesistiche della parabola
Intersezioni con gli assi
Determinare l'equazione
Carattesistiche della parabola
Se conosciamo l'equazione di una parabola, possiamo calcolarci facilmente l'equazione della direttrice e dell'asse, e le coordinate del fuoco e del vertice (vedi figura 3), mediante le seguenti formule:
Ricordiamo che Δ = b² − 4ac è il discriminante della parabola. Nella figura seguente è rappresentata una parabola generica con tutte le sue caratteristiche, secondo le formule scritte sopra, e gli eventuali punti di intersezione con gli assi cartesiani (vedi paragrafo seguente).
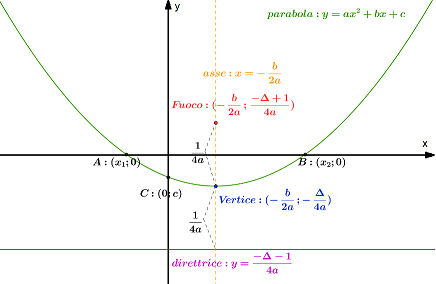Figura 3
|
Esempio 1. Determiniamo le caratteristiche della parabola di equazione:
y = x² + 4x + 3
Svolgimento. In questa equazione a=1, b=4, c=3. Quindi:
Δ = 4² − 4(1)(3) = 16 − 12 = 4
Partiamo dal vertice, essendo il punto più importante della parabola.
xV = − b ⁄ 2a = − 4 ⁄ 2 = − 2
yV = − Δ ⁄ 4a = − 4 ⁄ 4 = − 1
Il vertice ha coordinate V = (−2; −1). Di conseguenza l'asse di simmetria ha equazione:
x = − 2
Il fuoco possiede la stessa ascissa del vertice; l'ordinata si calcola:
yF = (−Δ+1) ⁄ 4a = (−4+1) ⁄ 4 = −3 ⁄ 4
Il fuoco ha coordinate F = (−2; −3 ⁄ 4).
Infine calcoliamo l'equazione della direttrice.
y = (−Δ−1) ⁄ 4a
y = (−3−1) ⁄ 4
y = −5 ⁄ 4
Conclusione: le caratteristiche della parabola sono:
- V = (−2; −1)
- a: x = − 2
- F = (−2; −3 ⁄ 4)
- d: y = −5 ⁄ 4
|
^
Torna su
Intersezioni con gli assi
Per determinare i punti di intersezioni con gli assi, si deve studiare il sistema tra l'equazione della parabola e le equazioni degli assi.
Per l'asse y il sistema è tra le equazioni y = ax² + bx + c e x = 0, che si risolve con y = c; il punto di intersezione esiste sempre, e ha coordinate (0, c).
Per l'asse x il sistema è tra le equazioni y = ax² + bx + c e y = 0, che si risolve
studiando l'equazione di II grado:
ax² + bx + c = 0
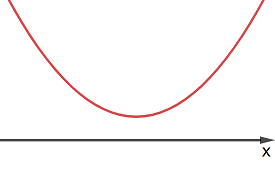
Esistono punti di intersezioni se e solo se quest'equazione ha soluzioni, ovvero se Δ ≥ 0; viceversa calcolare le soluzioni di un'equazione di II grado corrisponde a studiare le intersezioni tra una parabola e l'asse x.
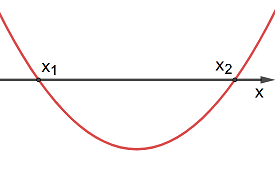
Se esistono due soluzioni dell'equazione, x1 e x2, allora esistono due punti d'intersezione di coordinate (x1, 0) e (x2, 0).
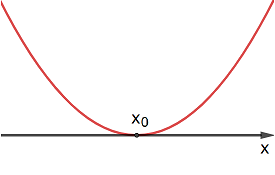
Se l'equazione ha soluzioni coincidenti, ovvero se Δ = 0, allora esiste un solo punto in comune tra parabola e asse x, ed è un punto di tangenza.
Possiamo quindi osservare che:
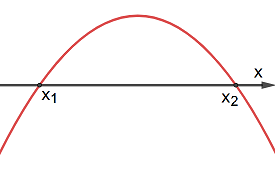
- Il coefficiente a rappresenta la curvatura della parabola: più grande è a, più stretta è la parabola; inoltre se a è positivo la parabola curva verso l'alto ed è tutta o quasi sopra l'asse x, se è negativo la parabola curva verso il basso ed è tutta o quasi sotto l'asse x.
- Il coefficiente b indica l'inclinazione della parabola nel punto d'intersezione con l'asse y e influisce quindi sull'equazione dell'asse di simmetria: maggiore è il valore assoluto di b, più l'asse della parabola è lontano dall'asse y.
- Il coefficiente c determina l'intersezione della parabola con l'asse y.
- Il Δ determina la presenza di intersezioni tra la parabola e l'asse x.
Nelle seguenti tabelle sono elencati esempi di grafici di parabole, in relazione al segno di a e Δ:
|
Esempio 2. Determiniamo le intersezioni con gli assi cartesiani della parabola vista in precedenza:
y = x² + 4x + 3
Svolgimento.
Asse x: poniamo la condizione y = 0.
Nell'equazione della parabola sostituiamo 0 al posto della y, ottendento l'equazione:
x² + 4x + 3 = 0
Risolvendo tale equazione, troviamo due soluzioni:
x1 = 1
x2 = 3
Ognuna di queste due soluzioni determina un punto di intersezione con l'asse delle x. Abbiamo quindi trovato i punti:
A = (1; 0)
B = (3; 0)
Asse y: poniamo la condizione x = 0.
Nell'equazione della parabola sostituiamo 0 al posto di ogni x, ottendento l'equazione:
y = (0)² + 4(0) + 3
Svolgendo i calcoli, troviamo la soluzione:
y = 3
Essa determina un punto di intersezione con l'asse delle y. Abbiamo quindi trovato un nuovo punto, di coordinate:
C = (0; 3)
Conclusione: questa parabola possiede tre punti di intersezione con gli assi cartesiani:
A = (1; 0), B = (3; 0), C = (0; 3)
|
^
Torna su
Condizioni per determinare l'equazione di una parabola
L'equazione di una parabola può esser determinata qualora si conoscano alcune informazioni su di essa; certe proprietà (come il vertice o il fuoco) sono più importanti e danno più informazioni; normalmente, qualora non si voglia determinare l'equazione di una parabola partendo da alcune sue proprietà, si parte dall'equazione canonica.
Nel caso in cui l'asse sia parallelo all'asse y:
y = ax² + bx + c
Nel caso in cui invece l'asse sia parallelo all'asse x:
x = ay² + by + c
Ecco alcuni esempi di condizioni per determinare l'equazione di una parabola, da combinare tra loro per formare un sistema con tre equazioni:
- si conosce un punto appartenente alla parabola: si applica la condizione di appartenenza, sostituendo le coordinate del punto nell'equazione canonica;
- si conoscono le coordinate del fuoco: il fuoco ci fornisce 2 condizioni, che possiamo utilizzare per costruire il sistema:
- x del fuoco: uguagliamo la formula per la x del fuoco al valore noto;
- y del fuoco: uguagliamo la formula per la y del fuoco al valore noto;
- si conosce l'equazione della direttrice: uguagliamo la formula per la direttrice al valore dell'equazione;
- si conoscono le coordinate del vertice: il vertice ci fornisce addirittura 3 condizioni, ma possiamo utilizzarle solo due, altrimenti otteniamo un sistema indeterminato:
- condizione di appartenenza: sostituiamo le coordinate del vertice nell'equazione canonica;
- x del vertice: uguagliamo la formula per la x del vertice al valore noto;
- y del vertice: uguagliamo la formula per la y del vertice al valore noto;
- si conosce l'equazione dell'asse: uguagliamo la formula per l'asse al valore dell'equazione;
- si conosce una retta tangente: si pone la condizione di tangenza: in un sistema a parte, si confrontando l'equazione della retta e l'equazione canonica della parabola, e nell'equazione risultante si studia il delta, ponendolo uguale a zero;
- si conosce la retta a cui appartiene il vertice: si applica la condizione di appartenenza, sostituendo le formule del vertice nell'equazione della retta.
|
Esempio 3. Determiniamo l'equazione della parabola con asse parallelo all'asse y, avente vertice di coordinate V (−2; 1) e passante per il punto A (0; −3).
Svolgimento. Il nostro obiettivo è trovare il valore dei coefficienti a, b, c presenti nell'equazione canoca:
y = ax² + bx + c
Dobbiamo quindi costruire le tre equazioni da mettere a sistema.
Prima condizione: appartenenza del vertice alla parabola: sostituiamo le coordinate del vertice nell'equazione canonica.
1 = a(−2)² + b(−2) + c
1 = 4a − 2b + c
Seconda condizione: x del vertice: uguagliamo la formula per la x del vertice al valore noto.
−b = − 4a
b = 4a
Terza condizione:appartenenza del punto A alla parabola: sostituiamo le coordinate del punto A nell'equazione canonica.
−3 = a(0)² + b(0) + c
−3 = c
c = −3
A questo punto costruiamo il sistema con le tre equazioni trovate.
⎧ 1 = 4a − 2b + c
⎨ b = 4a
⎩ c = − 3
In questi sistemi conviene sempre partire dalle equazioni più semplici, per sostituirle in quelle più avanzate; nel nostro caso possiamo osservare che la seconda e la terza equazione sono le più semplici, già esplicitate in funzione di a; sostituiamo quindi queste due equazioni nella prima, ottenendo:
1 = 4a − 2(4a) + (−3)
1 = 4a − 8a − 3
− 4a + 8a = − 1 − 3
4a = − 4
a = − 1
Una volta risolta l'equazione, è sufficiente risostituire il valore trovato per determinare quelli ancora incogniti, in questo caso la b:
b = 4a
b = 4 (−1)
b = − 4
Abbiamo risolto il sistema:
⎧ a = − 1
⎨ b = − 4
⎩ c = − 3
Conclusione: la parabola richiesta ha equazione:
y = − x² − 4x − 3
|
^
Torna su
<<< Precedente -
Successivo >>>
|
