Equazione canonica - Proprietà principali - Iperboli particolari

★ ★ ☆

<<< Precedente   -   Successivo >>>

Iperbole equilatera
Iperbole riferita ai propri asintoti
Funzione omografica

Iperbole equilatera

Un'iperbole è detta equilatera se gli asisntoti sono perpendicolari tra loro.
In un'iperbole equilatera si ha a = b, quindi l'equazione di un'iperbole equilatera con i fuochi sull'asse x e il centro nell'origine diventa:

che si può scrivere nella forma più comoda:

Un'iperbole equilatera ha le seguenti caratteristiche:

• i vertici hanno coordinate (±a, 0)
• i fuochi hanno coordinate (±√2a, 0)
• le direttrici hanno equazione x = ±(√2 ⁄ 2) a
• gli asintoti hanno equazione y = ±x
• l'eccentricità vale √2

Se a = 1, l'iperbole ha la seguente semplice equazione:

x² − y² = 1

^
Torna su

Iperbole riferita ai propri asintoti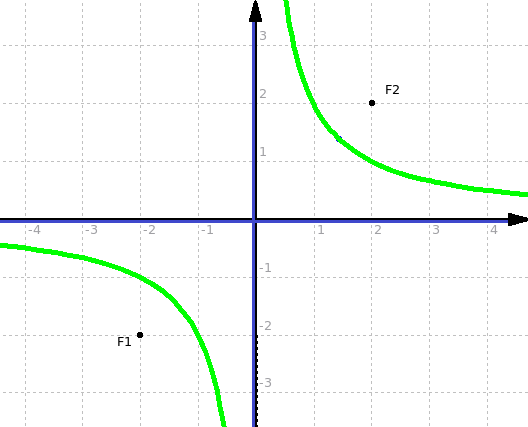

Possiamo cambiare sistema di riferimento, considerando gli asintoti dell'iperbole equilatera come nuovi assi cartesiani (figura 5).
Tale cambiamento è ottenibile con una rotazione di 45° in senso anti-orario:

X = (√2 ⁄ 2) · (x + y)

Y = (√2 ⁄ 2) · (y − x)

Nel nuovo sistema di riferimento l'equazione di un'iperbole equilatera diventa ancora più semplice:

essendo k = a² ⁄ 2; i fuochi e i vertici non si trovano più sugli assi cartesiani, bensì sulla bisettrice del 1° e 3° quadrante.
Un'iperbole equilatera in tale sistema è detta riferita ai propri asintoti e ha le seguenti caratteristiche:

• i vertici hanno coordinate (−√k, −√k) e (√k, √k)
• i fuochi hanno coordinate (−√2k, −√2k) e (√2k, √2k)
• le direttrici hanno equazione y = −x ±√k
• gli asintoti coincidono con gli assi cartesiani
• l'eccentricità vale √2 (non varia per isometrie)

^
Torna su

Funzione Omografica

Si chiama Funzione Omografica un'iperbole equilatera avente per asintoti due rette parallele agli assi cartesiani (figura 6); tale funzione è quindi ottenibile dalla curva precedente, mediante una traslazione di un vettore (α, β):

X = x − α

Y = y − β

Nel nuovo sistema di riferimento l'equazione diventa:

(x − α)(y − β) = k

ed esplicitando la y a sinistra, si ottiene a destra una frazione algebrica in x:

Nel caso in cui α, β o k siano delle frazioni, possiamo moltiplicare numeratore e denominatore per una qualunque quantità c ≠ 0, applicando la proprietà inveriantiva:

Così da ottenere tutti coefficienti interi. Una volta svolti i calcoli, otteniamo una equazione del seguente tipo:

Nella quale sono state applicate le seguenti sostituzioni:

• a = βc
• b = ck − αβc
• d = − αc

Da cui possiamo anche ricavare le formule inverse:

• α = − d ⁄ c
• β = a ⁄ c
• k = (bc − ad) ⁄ c²

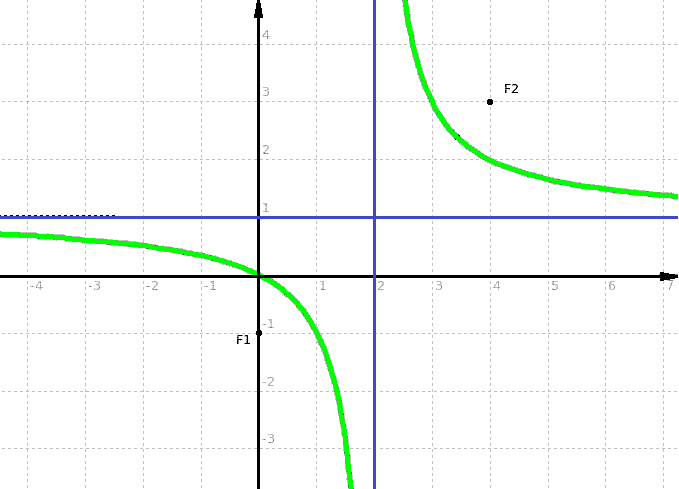
L'equazione che abbiamo ottenuto è l'equazione canonica della funzione omografica, e rappresenta una funzione algebrica razionale fratta, con numeratore e denominatore di primo grado.

La funzione omografica, essendo un'iperbole equilatera, possiede due asintoti perpendicolari tra loro (vedi figura 6) che in questo caso sono rette parallele agli assi cartesiani e hanno equazione:

^
Torna su

<<< Precedente   -   Successivo >>>