Introduzione - Linearità - Vettori componenti - Prodotti tra vettori - Momenti

★ ★ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Il momento di un vettore

Il momento di un vettore

I vettori in fisica hanno come applicazione principale la descrizione e lo studio del movimento, essendo usati per descrivere grandezze come lo spostamento, la velocità, la forza, ecc. Un particolare impiego consiste anche nello studio della rotazione dei corpi.

Ricordiamo che, dal punto di vista geometrico, una rotazione è una trasformazione che conserva costante la distanza di ogni punto P del piano da un punto fisso O chiamato centro di rotazione, facendo variare P nel punto P', tale l'angolo PÔP' corrisponda ad un valore prefissato (per approfondire, vedi le rotazioni).

Dal punto di vista fisico, il punto O è sempre il centro di rotazione, mentre il punto P che si sposterà in P' è il punto di applicazione del vettore.

Introduciamo quindi la seguente grandezze:

Il raggio e il braccio indicano quanto distante dal centro viene applicata la forza. Ovviamente non sono costanti, in quanto dipendono sia da qual è il centro di rotazione, sia da dove viene applicato il vettore: più distanti saranno questi due punti, maggiore saranno il raggio e il braccio. Definiamo a questo punto una grandezza molto importante in meccanica: il momento di un vettore.

Poiché il momento m è definito dal prodotto vettoriale, possiamo ricavare le sue caratteristiche seguendo le regole vista in precedenza; in particolare si ottiene che:

• la direzione di m è perpendicolare al piano su cui avviene la rotazione;
• il verso di m è uscente dal piano se la rotazione è antioraria, entrante se è oraria;
• il modulo di m è dato da:

Essendo α l'angolo tra la direzione del raggio e quella del vettore. Inoltre, ricordando i vettori componenti, possiamo osservare che:

|r| · sen(α) = r_⊥ = b

ossia il braccio, essendo la distanza tra il centro di rotazione e la retta-direzione di v, corrisponda ad r_⊥, la componente di r perpendicolare a v, come mostrato in figura 9, nella quale: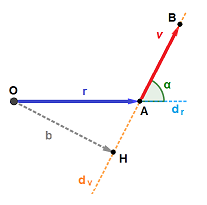

• Il vettore v (rosso) è applicato al punto A e ha per direzione la retta d _v (arancione).
• Il punto O è il centro di rotazione, quindi il vettore r = OA (blu) è il raggio di v e ha per direzione la retta d _r (azzurra).
• L'angolo tra i due vettori è α (verde), che si ottiene tra le rette r ed s.
• L'angolo OÂH è opposto al vertice (e quindi congruente) ad α.
• Il vettore b = r_⊥ = OH (grigio) del triangolo OAH è il braccio; essendo il cateto opposto ad α, si ha: b = |r| · sin(α)
• Il momento m in questa figura è un vettore che parte da O, perpendicolarmente al piano, con verso entrante, poiché per ruotare b verso v dobbiamo girare in senso orario.

Inoltre, poiché il prodotto vettoriale non è commutativo, non è possibile scambiare il braccio con il vettore: prima c'è il braccio, poi il vettore.

Importanti applicazioni del momento sono:

• il momento meccanico → il momento del vettore forza (clicca qui);
• il momento angolare → il momento del vettore quantità di moto (clicca qui).

^
Torna su

<<< Precedente   -   Successivo >>>