Introduzione - Linearità - Vettori componenti - Prodotti tra vettori - Momenti

★ ☆ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Somma tra vettori
Prodotto di un vettore per uno scalare
Combinazioni lineari
Differenza tra vettori

Somma tra vettori

La somma di due vettori è un vettore che corrisponde all'azione di entrambi i vettori, uno dopo l'altro:

u + v = w

Il vettore w che si ottiene dalla somma di due vettori si chiama vettore risultante.
Le coordinate del vettore risultante corrispondono alla somma algebrica delle coordinate dei singoli vettori addendi, ad esempio:

(5, -7, 0, 3) + (1, 3, -1, 5) = (6, -4, -1, 8).

Ovviamente possono esser sommati tra loro solo vettori di uguale dimensione.

Dal punto di vista grafico, possiamo costruire il vettore risultante applicando due regole equivalenti:

◊   Regola del punto-coda   ◊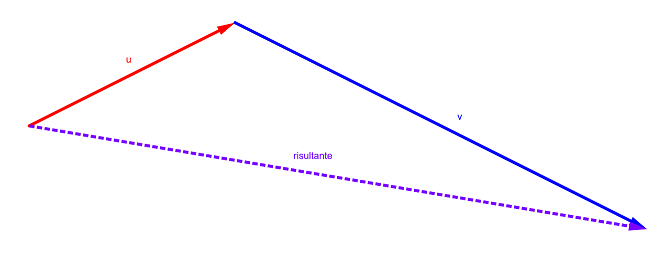

Per rappresentare il vettore risultante tra due vettori u e v, è sufficiente traslare uno dei due vettori in modo che la punta di u coincida con la coda di v: in questo modo le freccie dei due vettori sono consecutive.
Il vettore risultante corrisponde alla freccia che va dalla coda di u fino alla punta di v (figura 2).

◊   Regola del parallelogramma   ◊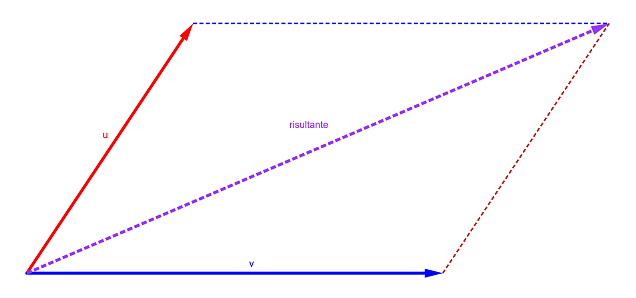

In alternativa, sempre per rappresentare il vettore risultante tra u e v, è possibile traslare uno dei due vettori in modo che le code di entrambi coincidano, e disegnare un parallelogramma avente e i lati paralleli ai due vettori.
Il vettore risultante corrisponde alla freccia che parte dalle code e, seguendo la diagonale del parallelogramma, arriva fino al vertice opposto (figura 3).

Il vettore nullo è un vettore formato da tutti zeri: sommato a qualunque vettore non ne cambia il risultato.

Un vettore è opposto ad un altro vettore se la loro somma dà il vettore nullo. Due vettori opposti hanno stessa direzione e stesso modulo, ma verso opposto.

^
Torna su

Prodotto di un vettore per uno scalare

Un'altra importante operazione è la moltiplicazione tra un vettore e uno scalare:

v · n = w

il vettore w si ottiene moltiplicando tutte le coordinate del vettore iniziale v per il numero n in questione; ad esempio:

(5, -7, 0, 3) · 3 = (15, -21, 0, 9)

Il vettore ottenuto è un multiplo del vettore iniziale, quindi i due vettori sono paralleli: la moltiplicazione per uno scalare influenza il modulo del vettore ma non la direzione; in particolare:

• il modulo si ottiene moltiplicando il modulo del vettore iniziale per lo scalare: |w| = |v| · n
• la direzione di w è la stessa di v
• il verso di w è lo stesso di v se lo scalare n è un numero positivo, al contrario se n è un numero negativo è opposto.

Se moltiplichiamo un vettore per il numero 0, otteniamo il vettore nullo.

Se moltiplichiamo un vettore per il numero -1, otteniamo il vettore opposto.

^
Torna su

Combinazioni lineari

Usando queste due operazioni introdotte sopra, possiamo definire alcuni importanti concetti:

Ad esempio il vettore (2, 6) è linearmente dipendente con i vettori (1, 1) e (0, 4), in quanto:

2 · (1, 1) + (0, 4) = (2, 6)

Al contrario il vettore (1, 2, 3) è linearmente dipendente con i vettori (1, 0, 0) e (0, 2, 0), in quanto la terza componente non potrà mai esser eguagliata.

Un esempio classico di base sono i due vettori canonici (1, 0) e (0, 1), che tra loro sono indipendenti e un qualunque altro vettore del piano può esser ottenuto da una combinazione di tali vettori.

^
Torna su

Differenza tra vettori

La differenza tra due vettori è un vettore che sommato al secondo, dà come risultante il primo:

u − v = w   ⇒   w + v = u

Il vettore w differenza tra i due vettori u e v si ottiene sommando al primo vettore l'opposto del secondo vettore.
Le coordinate del vettore risultante corrispondono alla differenza algebrica tra le coordinate dei singoli vettori, ad esempio:

(10, 3, 4, -5) − (0, 3, 1, -2) = (10, 0, 3, -3).

Ovviamente anche in questo caso i vettori devono avere uguale dimensione.

Dal punto di vista grafico, possiamo costruire il vettore risultante applicando la seguente regola: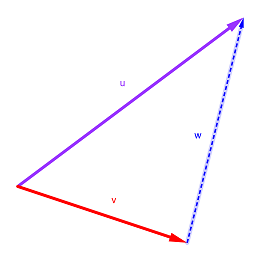

◊   Regola della differenza   ◊

Per rappresentare il vettore differenza tra due vettori u e v, è possibile traslare uno dei due vettori in modo che le code di entrambi coincidano.
Il vettore risultante corrisponde alla freccia che parte dalla punta del secondo vettore e arriva fino alla punta del primo vettore (figura 4).

La differenza tra due vettori uguali corrisponde al vettore nullo.

Osserviamo che la differenza tra due vettori è un semplice esempio di combinazione lineare.

^
Torna su

<<< Precedente   -   Successivo >>>