Introduzione - Linearità - Vettori componenti - Prodotti tra vettori - Momenti

★ ☆ ☆

<<< Precedente   -   Successivo >>>

CONTENUTO DELLA PAGINA
Le componenti di un vettore
Componenti parallele e perpendicolari

Le componenti di un vettore

La risultante tra più vettori genera un vettore linearmente dipendente ai vettori dati; possiamo fare il ragionamento inverso: dato un vettore risultante, è possibile risalire ai vettori che lo hanno generato?
No, dal momento che vi possono esser infinite possibilità!

Ad esempio: il vettore (2, 5) può esser il risultato di (2, 0) + (0, 5), ma anche di (1, 2) + (1, 3) o anche di altre coppie di vettori.

Possiamo però esser più pignoli e chiederci: dato un vettore risultante, è possibile ottenere un insieme di vettori di direzione fissata, che lo generano?
Nel piano a due dimensioni la domanda diventa: dato un vettore e due rette incidenti, è possibile trovare due vettori paralleli a tali rette che sommati diano il vettore iniziale? Risposta: Sì.

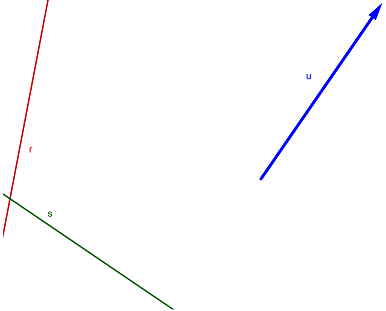
Nella figura 5 la situazione iniziale: due rette incidenti r ed s, ed un vettore u.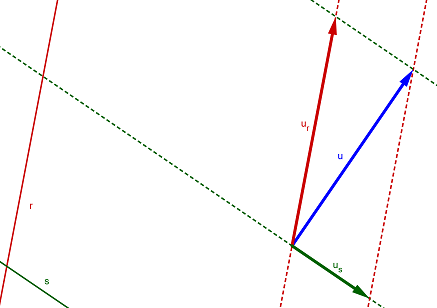
Per costruire graficamente i vettori u_r e u_s dobbiamo disegnare le rette parallele a quelle date, che passino per la coda del vettore e poi per la punta del vettore.

L'obiettivo è quello di costruire un parallelogramma con tali rette parallele intorno al vettore: i lati del parallelogramma adiacenti alla coda del vettore individuano i vettori componenti. Il risultato è mostrato nella figura 6.

Come abbiamo visto, le componenti cartesiane di un vettore sono i numeri che lo compongono, le coordinate cartesiane che ci aiutano per rappresentarlo graficamente e per svolgere le operazioni.
Possiamo scomporre un vettore nella somma di tanti vettori più componenti, ognuno focalizzato su una sola componente cartesiana del vettore iniziale, mentre le altre tutti zeri, ad esempio:

(4, − 2, 1, 8) = (4, 0, 0, 0) + (0, − 2, 0, 0) + (0, 0, 1, 0) + (0, 0, 0, 8)

Inoltre dalle componenti individuate possiamo utilizzare i versori canonici, e scrivere:

(4, − 2, 1, 8) = 4 (1, 0, 0, 0) − 2 (0, 1, 0, 0) + 1 (0, 0, 1, 0) + 8 (0, 0, 0, 1) =

= 4 v₁ − 2 v₂ + 1 v₃ + 8 v₄

Così facendo, abbiamo ottenuto vettori componenti semplici, ognuno appartenente ad una direzione canonica, ad un determinato asse.

Osserviamo che in generale ogni componente può esser vista come un multiplo di un versore, e ogni vettore può esser scritto come una combinazione lineare di versori, ad esempio nel caso di due dimensioni:

(5, 4) = 5 i + 4 j

^
Torna su

Componenti parallele e perpendicolari

Un'applicazione molto frequente dell'utilizzo di vettori componenti è nelle situazioni in cui si vuole decomporre un vettore lungo direzioni perpendicolari tra loro (come ad esempio gli assi cartesiani).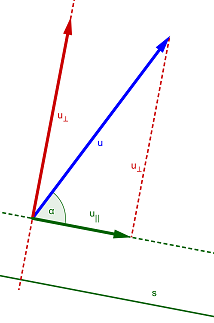

In fisica questo avviene ogni volta che un vettore (accelerazione, forza...) è "storto" rispetto alla direzione del moto, per cui ci sarebbe più comoda una sua componente parallela al moto. Altre volte invece c'è utile una componente perpendicolare al moto.

Nella figura 7 abbiamo disegnato le componenti del vettore u lungo la direzione parallela alla retta s u_∣∣ (in verde) e in quella perpendicolare u_⊥ (in rosso); il vettore u forma un angolo α con la direzione di s.

Osserviamo che si viene a formare un triangolo rettangolo avente come ipotenusa il vettore u e come cateti i vettori componenti u_⊥ e u_∣∣, e un angolo acuto ampio α.

Per non fare confusione con i termini:

• i vettori componenti sono due vettori che, sommati, danno il vettore iniziale;
• le componenti di un vettore sono i valori numerici, le intensità dei vettori componenti.

Applicando le formule goniometriche sui triangoli rettangoli, possiamo calcolare la lunghezza dei due vettori componenti:

^
Torna su

<<< Precedente   -   Successivo >>>