|
★ ☆ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
Classificazione
Proprietà dei triangoli isosceli
Risultati importanti
Classificazione
I triangoli si possono classificare in base ai lati oppure anche in base agli angoli.
In base ai lati:
scaleno se ha tutti i tre lati diversi tra loro;
isoscele se possiede almeno una coppia di lati congruenti;
equilatero se tutti i tre lati sono congruenti tra loro.
|
Nel triangolo isoscele la base è il lato diverso dagli altri.
In base agli angoli:
acutangolo se ha tutti i tre gli angoli acuti;
rettangolo se uno dei tre angoli è retto;
ottusangolo se uno dei tre angoli è ottuso.
|
Nel triangolo rettangolo l'ipotenusa è il lato maggiore; i lati rimanenti sono detti cateti .
Possiamo combinare le due classificazioni, ottenendo 7 diversi casi; eccone un elenco con relativi esempi:
scaleno
acutangolo
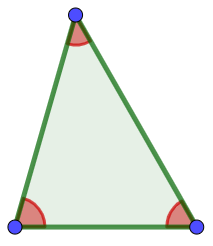
Figura 2 |
scaleno
rettangolo
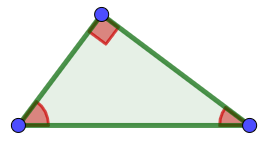
Figura 3 |
scaleno
ottusangolo
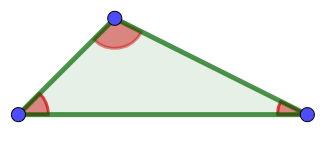
Figura 4 |
isocele
acutangolo
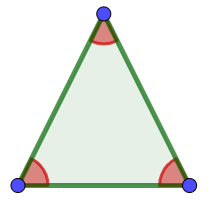
Figura 5 |
isocele
rettangolo
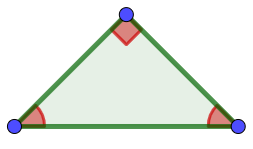
Figura 6 |
isocele
ottusangolo
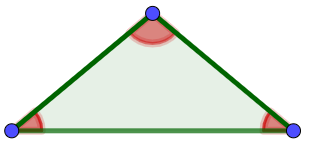
Figura 7 |
equilatero
(acutangolo)
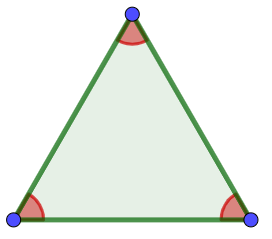
Figura 8 |
|
|
Osservazione: Il triangolo equilatero è un caso particolare di triangolo isoscele acutangolo; di conseguenza:
- ogni triangolo equilatero sicuramente è sia isoscele sia acutangolo;
- un triangolo isoscele acutangolo può esser anche equilatero;
- non esistono triangoli equilateri ottusangoli o rettangoli.
^
Torna su
Proprietà dei triangoli isosceli
Dai criteri di congruenza fra triangoli si possono ottenere delle proprietà importanti legati alla loro classificazione.
|
Teorema del triangolo isoscele
Ogni triangolo isoscele ha anche 2 angoli congruenti;
inoltre ogni triangolo avente 2 angoli congruenti è isoscele.
Elementi del triangolo isoscele
In un triangolo isoscele la mediana, la bisettrice e l'altezza relative alla base coincidono.
Teorema del triangolo equilatero
Ogni triangolo equilatero ha i 3 angoli congruenti;
inoltre ogni triangolo avente i 3 angoli congruenti è equilatero.
|
Il triangolo equilatero è un poligono regolare; le caratteristriche principali di un triangolo equilaretp di lato ℓ come poligono regolare sono:
- ampiezza degli angoli al centro: ω = 120°
- ampiezza degli angoli interi: α = 60°
- num. fisso per l'apotema: λ3 = 0,289…
- num. fisso per l'area: φ3 = 0,433…
- lunghezza dell'apotema: a = ⅙ ℓ √3
- lunghezza del raggio: r = ⅓ ℓ √3
- lunghezza dell'altezza: h = ½ ℓ √3
- numero di diagonali: nd = 0
- Area: A = ¼ ℓ² √3
^
Torna su
Risultati importanti sui triangoli qualunque
Ecco infine alcuni teoremi di fondamentale importanza per lo studio dei triangoli.
|
1° teorema dell'angolo esterno
In un triangolo ogni angolo esterno è maggiore di ciascuno dei due angoli interni non adiacenti.
Somma degli angoli interni
La somma degli angoli interni di un triangolo corrisponde ad un angolo piatto.
2° teorema dell'angolo esterno
In un triangolo ogni angolo esterno è uguale alla somma dei due angoli interni non adiacenti.
Relazioni tra lati e angoli
In ogni triangolo il maggiore tra i lati è opposto al maggiore tra gli angoli
e il minore tra i lati è opposto al minore tra gli angoli;
se due lati sono uguali anche gli angoli opposti sono uguali.
Perimetro
Il perimetro di un triangolo equivale alla somma dei suoi tre lati.
Area
L'area di un triangolo equivale al semiprodotto del lato di base per l'altezza ad esso relativa.
|
^
Torna su
<<< Precedente -
Successivo >>>
|






