|
★ ☆ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
I poligoni regolari
Formulario
Triangolo ♦
Quadrato ♦
Pentagono ♦
Esagono
Ettagono ♦
Ottagono ♦
Ennagono ♦
Decagono
Dodecagono ♦
Icosagono
I poligoni regolari
Un poligono avente tutti i suoi lati e tutti i suoi angoli interni congruenti tra loro è detto regolare ; ogni poligono regolare gode delle seguenti proprietà:
- ha tutti gli angoli esterni congruenti;
- ha gli angoli esterni congruenti agli angoli al centro;
- ha tutte le apoteme congruenti;
- ha tutti i raggi congruenti;
- è inscrivibile in una circonferenza;
- è circoscrivibile in una circonferenza;
I poligoni regolari sono figure molto particolari, che riccorrono spesso sia nei problemi scolastici, sia nella vita quotidiana, soprattutto nelle opere artistiche.
Una scorciatoia aritmetica per il calcolo dell'apotema e dell'area di poligoni regolari sono i numeri fissi : ogni poligono regolare possiede due numeri fissi, che qui indichiamo con λn e φn: sono valori costanti, conoscendo i quali possiamo calcolare apotema e area partendo dalla lunghezza ℓ del lato (vedi le regole di seguito).
^
Torna su
Formulario
Di seguito sono elencati sinteticamente i principali poligoni regolari, con le loro caratteristiche.
Ecco le principali caratteristiche di un generico poligono regolare:
|
Legenda:
- n : numero lati (tale numero dà il nome al poligono)
- ℓ : lato – segmento che unisce due vertici consecutivi
- h : altezza – segmento perpendicolare che unisce due lati, o un lato e un vertice
- a : apotema – raggio della circonferenza inscritta al poligono
- r : raggio – il raggio della circonferenza circoscritta al poligono
- ω : angolo al centro – angolo acuto tra due raggi consecutivi
- α : angolo interno – angolo convesso tra due lati consecutivi
- d : diagonale maggiore – il più lungo segmento che unisce due vertici del poligono
- d1, d2, … : altre diagonali – gli altri segmenti che uniscono due vertici del poligono non consecutivi
- nd : numero diagonali
- λn : numero fisso per l'apotema
- φn : numero fisso per l'area
- 2p : perimetro
- p : semiperimetro
- A : area del poligono
|
In generale, valgono le seguenti formule per calcolare le caratteristiche di un poligono regolare:
Applicando tali formule ad ogni poligono regolare, ottemiamo valori e formule personalizzate, per ogni figura; vediamo ora una classificazione dei principali poligoni regolari aventi lato ℓ assegnato.
^
Torna su
TRIANGOLO EQUILATERO
- n = 3
- ω = 120°
- α = 60°
- λ3 = 0,289…
- φ3 = 0,433…
- a = ⅙ ℓ √3
- r = ⅓ ℓ √3
- h = ½ ℓ √3
- nd = 0
- 2p = 3ℓ
- A = ¼ ℓ² √3
|
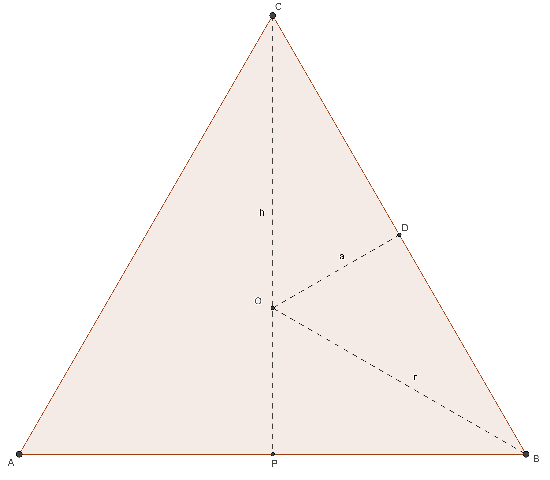 Triangolo equilatero
Triangolo equilatero
(3 lati)
|
QUADRATO
- n = 4
- ω = 90°
- α = 90°
- λ4 = 0,5
- φ4 = 1
- a = ½ ℓ
- r = ½ ℓ √2
- h = ℓ
- nd = 2
- d = ℓ √2
- A = ℓ²
|
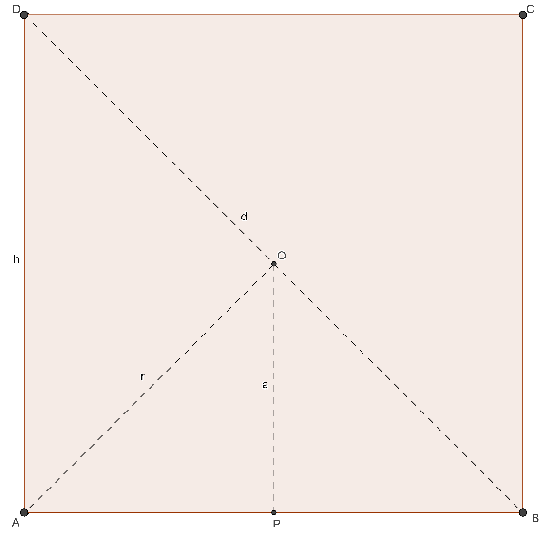 Quadrato
Quadrato
(4 lati)
|
PENTAGONO REGOLARE
- n = 5
- ω = 72°
- α = 108°
- λ5 = 0,688…
- φ5 = 1,720…
- a = ℓ √(5 + 2√5) / 20
- r = ℓ √(5 + √5) / 10
- h = a + r = ℓ √(5 + 2√5) / 2
- nd = 5
- d = ½ ℓ (1 + √5)
- A = ¼ ℓ² √(25 + 10√5)
|
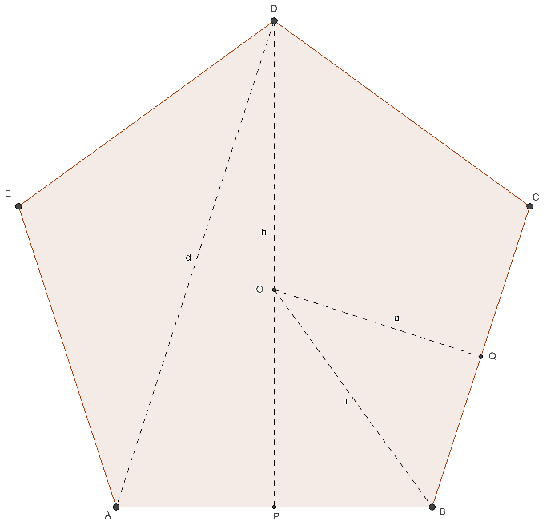 Pentagono regolare
Pentagono regolare
(5 lati)
|
ESAGONO REGOLARE
- n = 6
- ω = 60°
- α = 120°
- λ6 = 0,866…
- φ6 = 2,598…
- a = ½ ℓ √3
- r = ℓ
- h = 2 a = ℓ √3
- nd = 9 [3 maggiori]
- d = 2 r = 2 ℓ
- d1 = ℓ √3
- A = ½ ℓ² 3√3
|
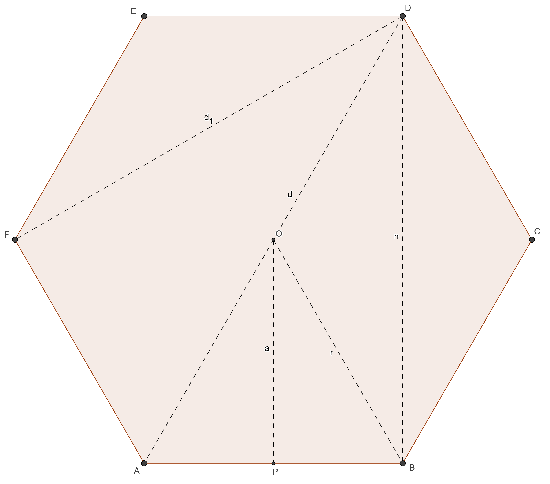 Esagono regolare
Esagono regolare
(6 lati)
|
^
Torna su
ETTAGONO REGOLARE
- n = 7
- ω = 51° 25' 43"
- α = 128° 34' 17"
- λ7 = 1,038…
- φ7 = 3,634…
- a = ½ ℓ cotg (180°/7)
- r = ½ ℓ cosec (180°/7)
- h = a + r
- nd = 14 [7 maggiori]
- d = √¼ ℓ² + h²
- A = 7 ℓ² cotg (180°/n) / 4
|
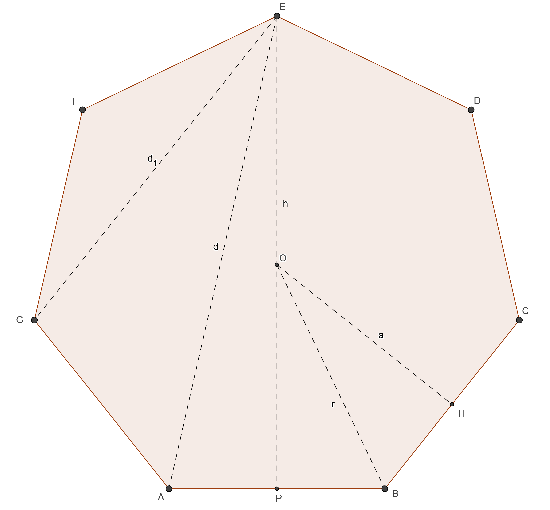 Ettagono regolare
Ettagono regolare
(7 lati)
|
OTTAGONO REGOLARE
- n = 8
- ω = 45°
- α = 135°
- λ8 = 1,207…
- φ8 = 4,828…
- a = ½ ℓ (1 + √2)
- r = ½ ℓ √(4 + 2√2)
- h = 2 a = ℓ (1 + √2)
- nd = 20 [4 maggiori]
- d = 2 r = ℓ √(4 + 2√2)
- d1 = 2 a = ℓ (1 + √2)
- d2 = ℓ √(2 + √2)
- A = 2 ℓ² (1 + √2)
|
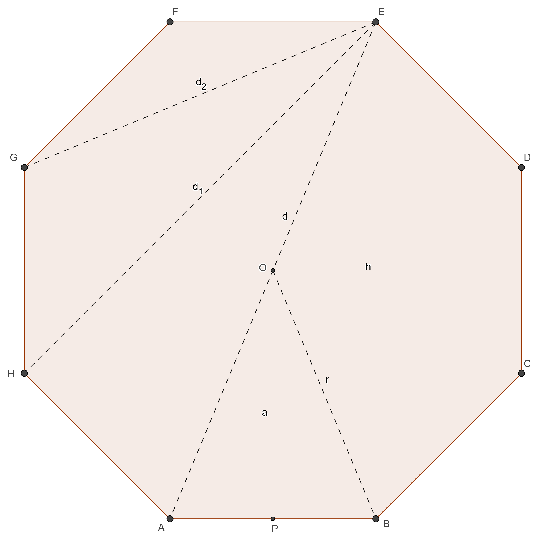 Ottagono regolare
Ottagono regolare
(8 lati)
|
ENNAGONO REGOLARE
- n = 9
- ω = 40°
- α = 140°
- λ9 = 1,374…
- φ9 = 6,182…
- a = ½ ℓ cotg (20°)
- r = ½ ℓ cosec (20°)
- h = a + r
- n9 = 27 [9 maggiori]
- d = √¼ ℓ² + h²
- A = 9 ℓ² cotg (20°) / 4
|
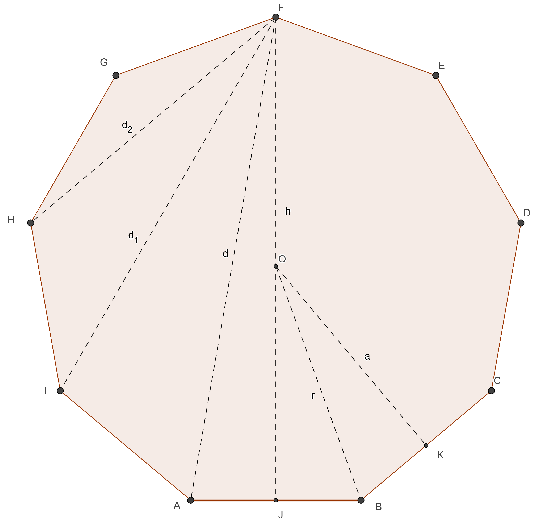 Ennagono regolare
Ennagono regolare
(9 lati)
|
DECAGONO REGOLARE
- n = 10
- ω = 36°
- α = 144°
- λ10 = 1,539…
- φ10 = 7,694…
- a = ½ ℓ √(5 + 2√5)
- r = ½ ℓ (1 + √5)
- h = 2 a = ℓ √(5 + 2√5)
- nd = 35 [5 maggiori]
- d = 2 r = ℓ (1 + √5)
- A = 5 ℓ² √(5 + 2√5) / 2
|
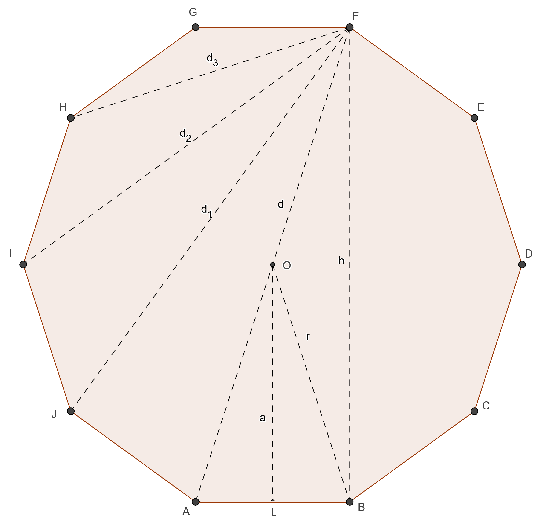 Decagono regolare
Decagono regolare
(10 lati)
|
^
Torna su
DODECAGONO REGOLARE
- n = 12
- ω = 30°
- α = 150°
- λ12 = 1,866…
- φ12 = 11,196…
- a = ½ ℓ (2 + √3)
- r = ½ ℓ (√2 + √6)
- h = 2 a = ℓ (2 + √3)
- nd = 54 [6 maggiori]
- d = 2 r = ℓ (√2 + √6)
- A = 3 ℓ² (2 + √3)
|
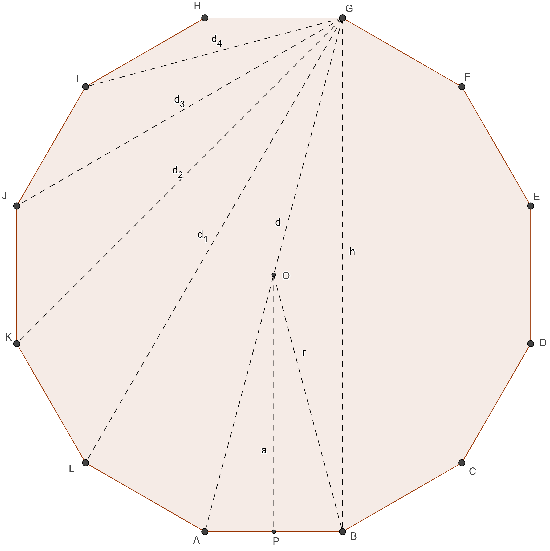 Dodacagono regolare
Dodacagono regolare
(12 lati)
|
ICOSAGONO REGOLARE
- n = 20
- ω = 18°
- α = 162°
- λ20 = 3,157…
- φ20 = 31,569…
- a = ½ ℓ cotg (9°)
- r = ½ ℓ cosec (9°)
- h = 2 a = ℓ cotg (9°)
- nd = 170 [10 maggiori]
- d = 2 r = ℓ cosec (9°)
- A = 5 ℓ² cotg (9°)
|
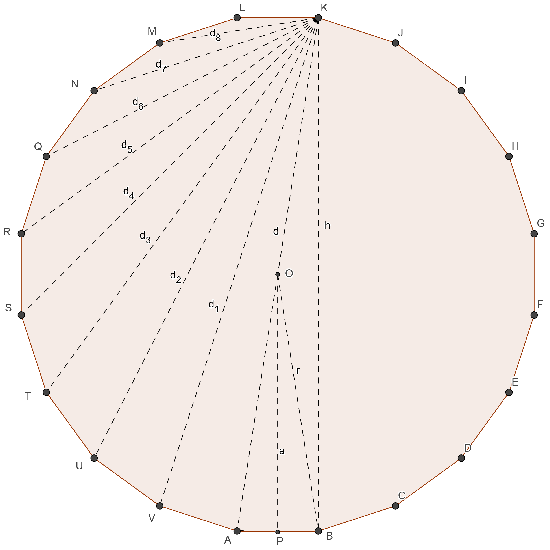 Icosagono regolare
Icosagono regolare
(20 lati)
|
^
Torna su
<<< Precedente -
Successivo >>>
|









