|
★ ★ ☆
<<< Precedente -
Successivo >>>
CONTENUTO DELLA PAGINA
Moto circolare uniforme
Moto circolare accelerato
Il moto circolare descrive il moto di un punto materiale P lungo una circonferenza di raggio R, in cui variano la posizione, la velocità e l'accelerazione, come vettori: quindi oltre a cambiare il valore numerico, cambiano anche la direzione e il verso di tali grandezze.
Moto circolare uniforme
Il moto circolare uniforme è un moto periodico lungo una circonferenza di raggio R, in cui posizione, velocità e accelerazione rimangono costanti in modulo, ma variano solamente in direzione e verso.
Due grandezze caratteristiche di un moto periodico sono:
- Il
Periodo (𝒯): l'intervallo di tempo che il corpo impiega a compiere un giro (o oscillazione) completo(a); si misura quindi in secondi.
- La
Frequenza (ƒ): il numero di giri (od oscillazioni) che il corpo compie in un secondo; la frequenza è quindi numericamente uguale al reciproco del periodo; si misura in Hertz (Hz).
In generale vale quindi la relazione:
Il moto circolare uniforme è la composizione di due moti armonici aventi la stessai frequenza: uno verticale e uno orizzontale, sfasati di un quarto di periodo.
Il vettore posizione è r = (x, y), dove x e y sono le coordinate del punto P; il modulo del vettore r è il raggio R della circonferenza; la posizione può esser descritta anche dalle coordinate polari (R, θ) dove θ l'angolo al centro che varia nel tempo; valgono le la relazioni:
- R² = x² + y²
- x = R cos(θ)
- y = R sen(θ)
data dal Teorema di Pitagora e dai teoremi goniometrici.
Le altre importanti grandezze che descrivono il moto circolare uniforme sono:
Velocità tangenziale vT: è la velocità istantanea del corpo che si muove lungo la circonferenza: nel moto circolare uniforme, come abbiamo detto, ha modulo costante; il modulo della velocità si può calcolare nei seguenti modi:
la direzione e il verso invece non sono costanti: la direzione è sempre tangente alla circonferenza e il verso segue quello del moto. La velocità tangenziale si misura in metri al secondo (m ⁄ s) come una qualunque velocità.
Velocità angolare ω: indica la variazione dell'angolo θ nel tempo: Δθ ⁄ Δt. Si ottiene come il prodotto vettoriale tra il raggio e la velocità istantanea: ω = r × vT.
Anche la velocità angolare è un vettore avente modulo costante; esso si può calcolare nei seguenti modi:
il modulo della velocità angolare corrisponde alla pulsazione dei moti armonici componenti. La direzione è perpendicolare al piano e passante per il centro della circonferenza; il verso è in alto se il moto è in senso antiorario e in basso se il moto è in senso orario (secondo la normale regola del prodotto vettoriale). La velocità angolare si misura in radianti al secondo (rad ⁄ s) e, dal momento che i radianti non hanno dimensioni fisiche, la velocità angolare ha le dimensioni di una frequenza, sebbene si misuri in modo diverso.
Accelerazione centripeta ac: l'accelerazione istantanea ha modulo costante, è si calcola:
la direzione è quella del raggio, e il verso punta sempre verso il centro. L'accelerazione centripeta si misura in metri al secondo quadrato (m ⁄ s²) come una qualunque accelerazione.
In figura 2 è riportata una rappresentazione del moto circolare di un punto P in un classico piano cartesiano Oxy, con i vettori posizione (in verde), velocità tangenziale (in blu) e accelerazione centripeta (in rosso).
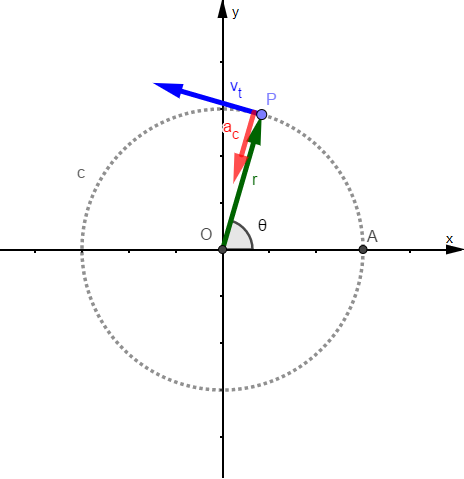 Figura 2
Figura 2
In questa figura la velocità angolare è un vettore che esce dal piano, partendo dal punto O.
Il moto circolare uniforme è la composizione di due moti armonici con uguale periodo e ampiezza d'oscillazione, ma sfasati di un quarto di periodo; le equazioni orarie del moto circolare uniforme sono:
|
Esempio 6. Un oggetto ruota di moto circolare uniforme su una traiettoria di raggio 3,00 m e con una frequenza di 5,00 Hz.
Calcoliamo la velocità tangenziale, la velocità angolare e l'accelerazione centripeta di tale oggetto.
Dati:
R = 3,00m
ƒ = 5,00Hz
vT = incognita
ω = incognita
ac = incognita
Soluzione: il raggio misura 3m, dunque la circonferenza descritta è lunga:
C = 2π · (3,00m) = 18,8m
La velocità tangenziale è quindi:
vT = 2πR ƒ = (18,8m) · (5Hz) = 94,0m/s
La velocità angolare è:
ω = 2π ƒ = 6,28 · (5Hz) = 31,4rad/s
Infine l'accelerazione centripeta corrisponde a:
ac = ω vT = (31,4rad/s) · (94,0m/s) = 2951,6m/s²
che arrotondato diventa: 2,95 · 10³ m/s²
Conclusione:
la velocità tangenziale vale 94,0m/s,
la velocità angolare 31,4rad/s
l'accelerazione centripeta 2,95 · 10³ m/s².
|
^
Torna su
Moto circolare accelerato
Moto di un punto P lungo una circonferenza di raggio R, in cui variano le caratteristiche vettoriali di spazio, velocità e accelerazione (anche in modulo).
Nel moto circolare accelerato la posizione r è sempre un vettore di modulo R, che parte dal centro e arriva alla posizione del punto P, le cui coordinate cartesiane sono (x, y) – oppure coordinate polari (R; θ).
L'equazione oraria è:
Dove θ(t) è una funzione che descrive come varia l'angolo θ nel tempo.
Grandezze coinvolte:
- Velocità angolare istantanea: ω(t) = dθ(t) ⁄ dt
ha direzione perpendicolare al piano e passante per il centro della circonferenza; il verso è in alto se il moto è in senso antiorario, e in basso se il moto è in senso orario.
- Velocità tangenziale istantanea: v(t) = R · dθ(t) ⁄ dt = ω(t) · R
ha direzione tangente alla circonferenza e verso del moto.
- Accelerazione istantanea: a(t) = R · d²θ(t) ⁄ dt²
è la somma vettoriale tra due accelerazioni: l'accelerazione centripeta (che ha direzione del raggio, verso il centro) e l'accelerazione tangenziale (che ha direzione tangente alla circonferenza; il verso è quello del moto se la velocità tangenziale aumenta, opposto se diminuisce).
Dove con la lettera d minuscola indichiamo una variazione infinitesima di una determinata grandezza (al contrario del Δ che indica una variazione visibile, misurabile); dal punto di vista matematico, il rapporto tra due variazioni infinitesime corrisponde alla derivata della grandezza che sta al numeratore, rispetto alla grandezza che sta al denominatore (per approfondire, vedi le pagine sulle derivate).
^
Torna su
<<< Precedente -
Successivo >>>
|
