| Inizio | News | DERIVATE | Info |
|
|
INTRODUZIONE ALLE DERIVATE <<< Precedente - Successivo >>> Il rapporto incrementale Il rapporto incrementale è il rapporto tra gli incrementi delle variabili, ossia quanto varia la y e quanto varia la x in una curva nel piano cartesiano: Δy / Δx. 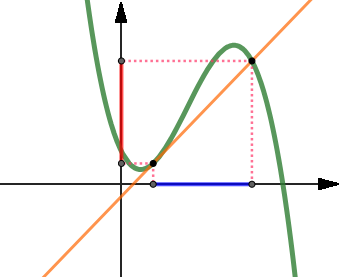 Studiamo una funzione continua ƒ e consideriamo un suo punto A, di coordinate: xA = x₀ e yA = ƒ(x₀) Per capire come varia tale funzione, ci spostiamo dal punto A ad un suo punto vicino B (sempre della funzione ƒ); esso ha coordinate: xB = x₀ + h; e yB = ƒ(x₀ + h) Di conseguenza: Possiamo quindi definire:
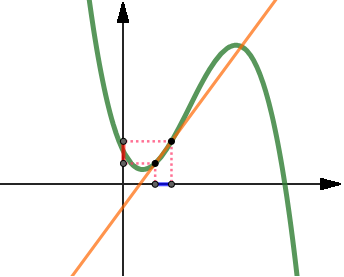 Il rapporto incrementale è molto utile perché coorisponde al coefficiente angolare m della retta y = mx + q che passa per i due punti assegnati, quindi ci dà indicazioni sull'andamento della funzione (come in fisica avviene quando calcoliamo la velocità media). Ad esempio se il rapporto incrementale tra A e B è positivo, vuol dire che la funzione tra A e B in media sta crescendo, mentre se è negativo sta in media scendendo. Tuttavia se vogliamo avere un risultato più accurato, dobbiamo far sì che i punti A e B siano molto vicini tra loro, ossia che la differenza h sia molto piccola, addirittura infinitesima. Il concetto di derivata Come abbiamo detto, se vogliamo avere un risultato più accurato, dobbiamo far sì che i punti A e B siano molto vicini tra loro. 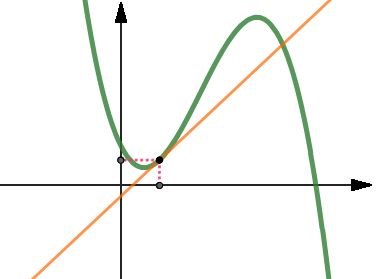 In situazioni di questo tipo sia Δx, sia Δy si avvicinano a 0, quindi non si possono svolgere i calcoli normalmente, in quanto non si può dividere per zero. Per questo motivo è necessario studiare il limite del rapporto incrementale per h → 0 e verificare se il risultato venga un valore numerico finito (il coefficiente angolare non può esser infinito). Spesso studiando tale limite si ottiene una forma indeterminata 0 / 0. Se risolvendo la forma indeterminata si verifica che il limite esiste ed è un numero reale finito, allora:
Di conseguenza la derivata in un punto ci dice la pendenza della curva in quel punto.
Dal punto di vista geometrico, vale questa importantissima proprietà:
Il calcolo della funzione derivata o, più semplicemente, della derivata avviene tramite regole e procedure specifiche; in effetti il termine derivata può significare in generale l'operatore, ossia la funzione che modifica altre funzioni, secondo tali regole. D: ƒ ↦ ƒ ' Esistono infatti delle formule che ci consentono di calcolare la derivata in un punto generico di una funzione, senza fare lo studio del limite: si parte dallo studio della derivata di funzioni semplici e si esamina cosa succede alla derivata componendo tra loro più funzioni. Il concetto di differenziale Un altro concetto molto importante e strettamente legato alla derivata è quello di differenziale. Il differenziale di una variabile x si scrive dx, ed equivale ad una variazione infinitesima della x, ossia ad un Δx molto piccolo. Analogamente il In pratica il differenziale corrisponde al limite del numeratore del rapporto incrementale. Per questo la derivata, essendo il limite del rapporto incrementale, può esser vista come il rapporto tra due differenziali:
In altri termini: scriviamo la derivata di una funzione non come il limite di un rapporto, ma come un rapporto tra due limiti. Rigirando questa formula, possiamo scrivere il differenziale di una funzione:
Tale formula è molto utile nello studio degli integrali. <<< Precedente - Successivo >>> |
| Condizioni di utilizzo | Contatti | Created by Stefano Caroselli | Mappa |